Qué son las sucesiones y progresiones
Profundiza en las sucesiones y progresiones gracias a esta guía con los recursos y materiales más destacados de la unidad de Math Bits.
19 de noviembre de 2023

Una experiencia tan próxima a nosotros como la evolución de una pandemia, por ejemplo, nos puede introducir en el mundo de las sucesiones y progresiones. La unidad permitirá al alumnado, gracias a estos objetos matemáticos, desarrollar competencias específicas relacionadas con la resolución de problemas. Además, observaremos cómo la generalización, el reconocimiento de patrones, la comunicación y la representación juegan un papel fundamental en el proceso de explorar las conexiones matemáticas detrás de fenómenos de la vida real.
Todo ello en torno a grandes ideas que se enmarcan en el sustrato del cálculo y el análisis, pues los conceptos de límite y convergencia planearán a lo largo de la secuencia.
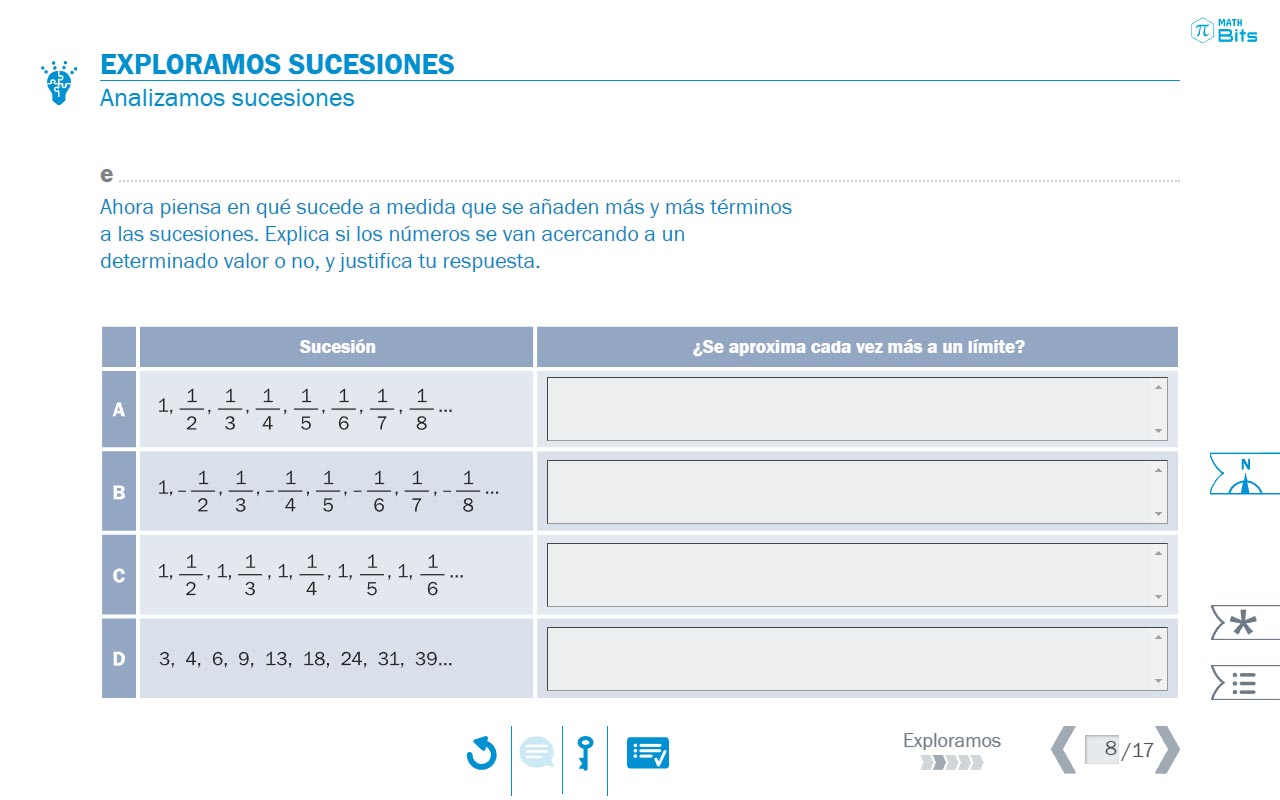
Como siempre, los planos de abstracción se introducen gradualmente, ofreciendo oportunidades diversas para conectar con los significados y las intuiciones personales del estudiante. Así, en la primera actividad de exploración, después de tratar de encontrar cómo continúan algunas sucesiones a partir de sus términos iniciales, nos detenemos a describir el crecimiento de estas en detalle. Las sucesiones han sido elegidas convenientemente para abordar la convergencia y los diferentes tipos de no convergencia (límite infinito y oscilación).
- Sucesiones numéricas con diversos tipos de crecimiento..
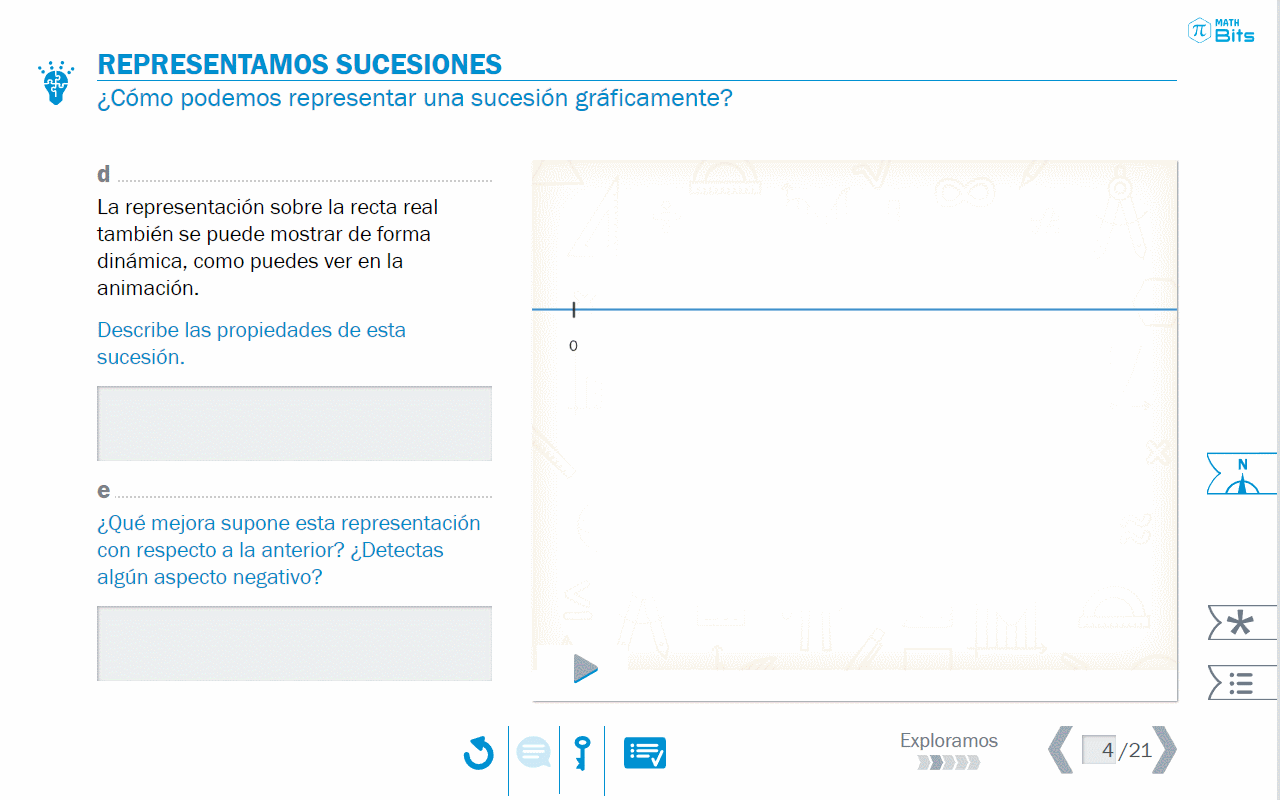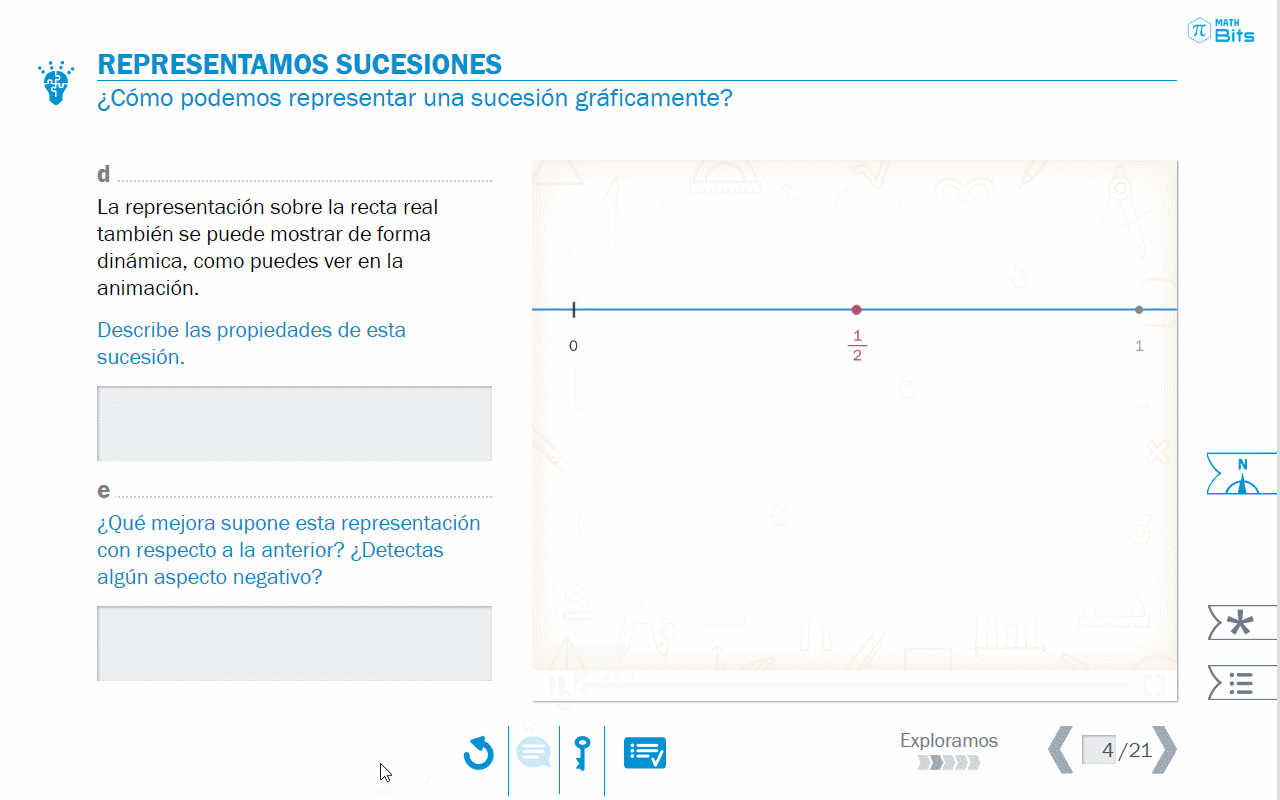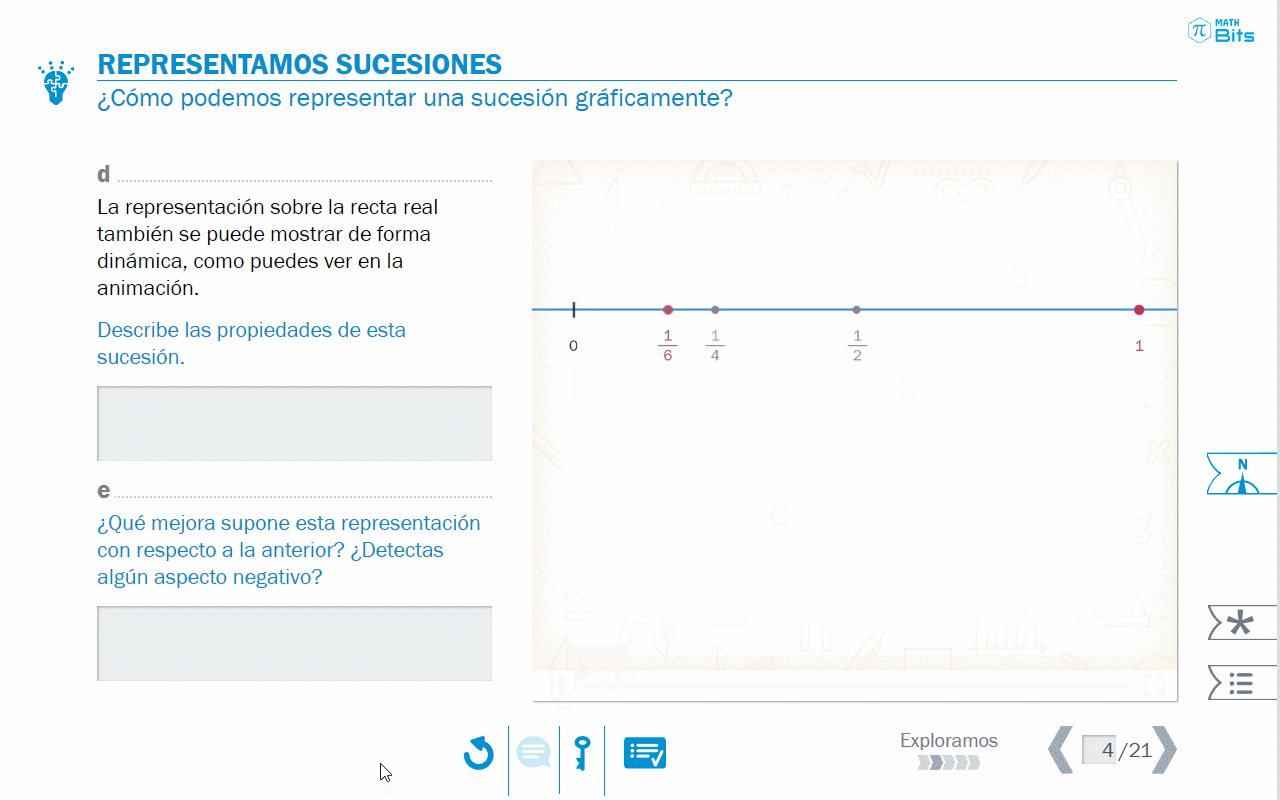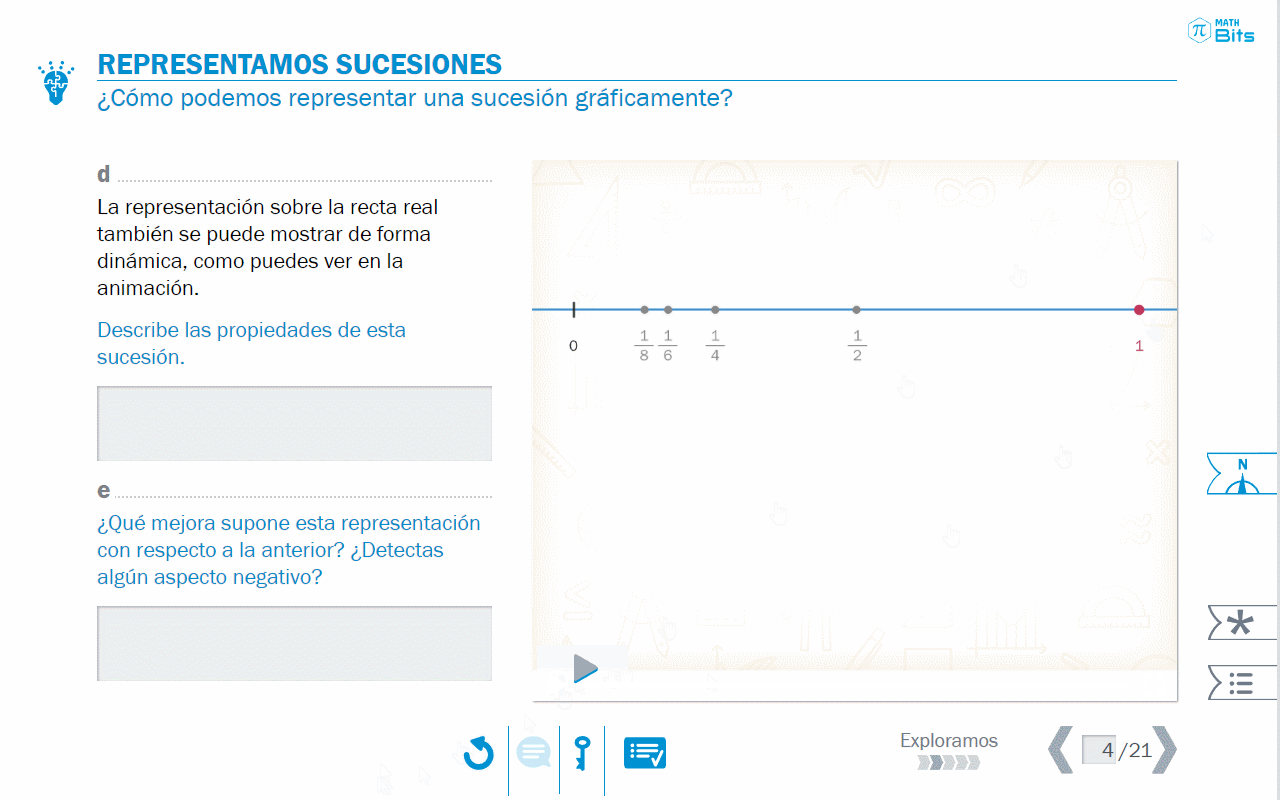
A continuación, la secuencia explora el registro gráfico, poniendo sobre la mesa, en primer lugar, la adecuación de la representación elegida.
Posteriormente, se abordan la monotonía y la convergencia de las sucesiones desde el registro gráfico, lo que aporta una visión más completa en términos de significado.
- Registro gráfico para explorar el crecimiento de sucesiones numéricas.
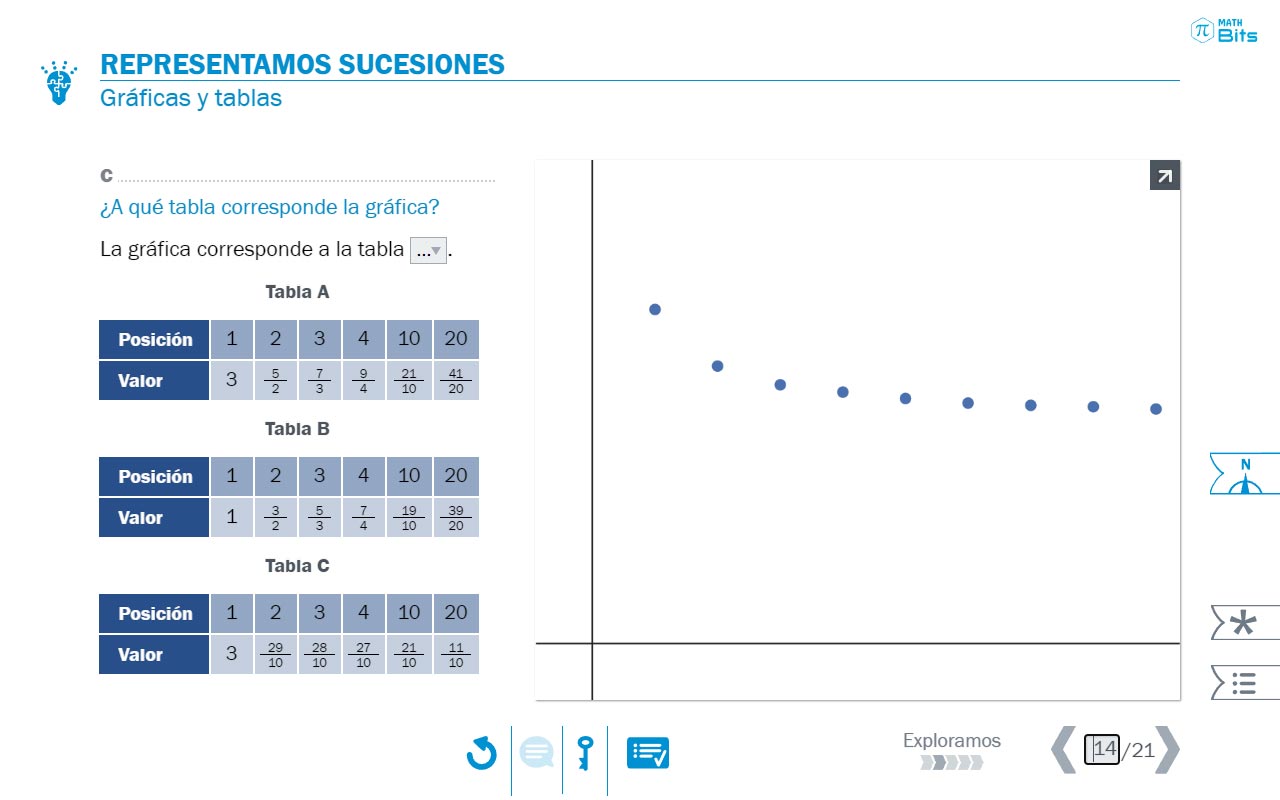
Precisamente, las conversiones directas de registro de representación van a ayudar mucho en la construcción progresiva de significado. Así pues, se plantean tareas en las que el alumnado debe pasar de un registro a otro (por ejemplo, de tabular a gráfico) sin pasar por otro intermedio (por ejemplo, el algebraico).
- Conversiones entre registro tabular y gráfico.
Una vez que se ha movilizado el lenguaje verbal suficiente para describir el comportamiento de una sucesión y se han articulado las conversiones entre registros, es el momento de abordar el registro algebraico. De esta manera, el alumnado puede apreciar la necesidad del álgebra para describir de forma precisa la regla de formación, es decir, el término general de una sucesión.
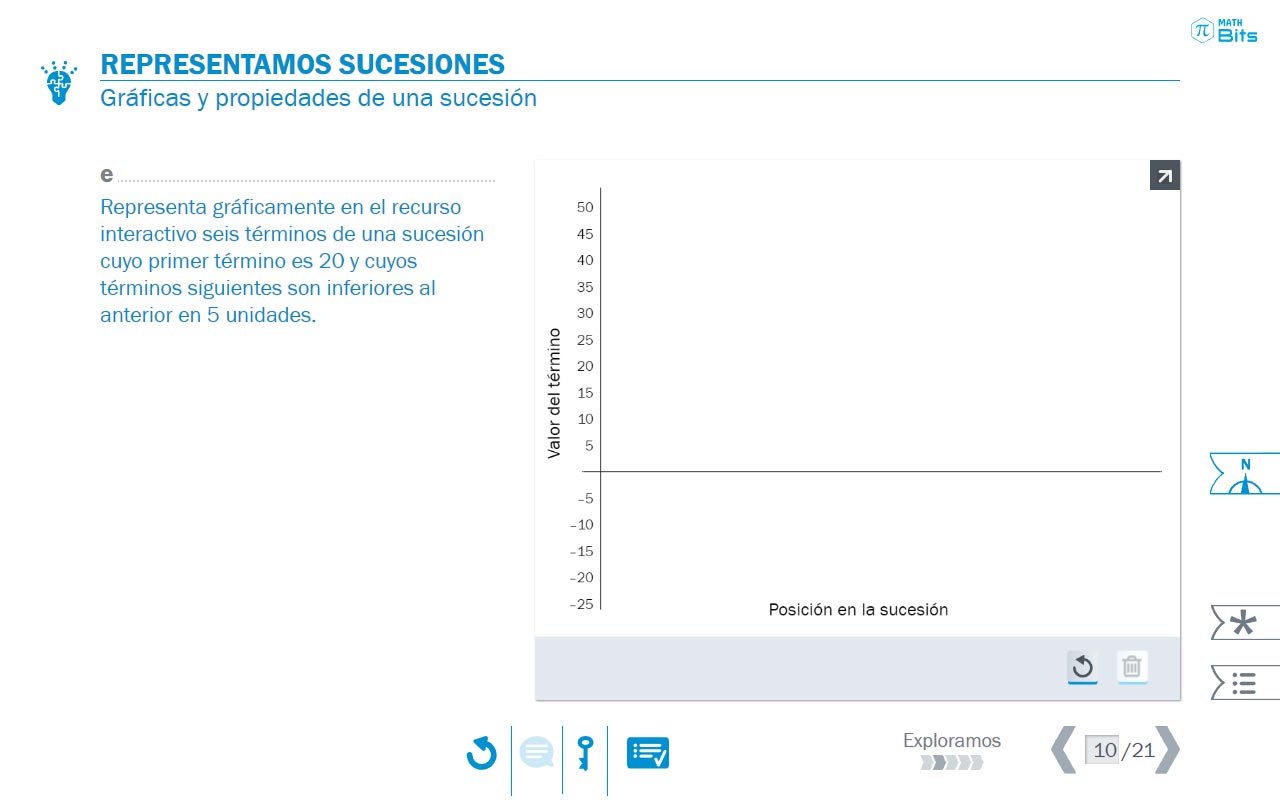
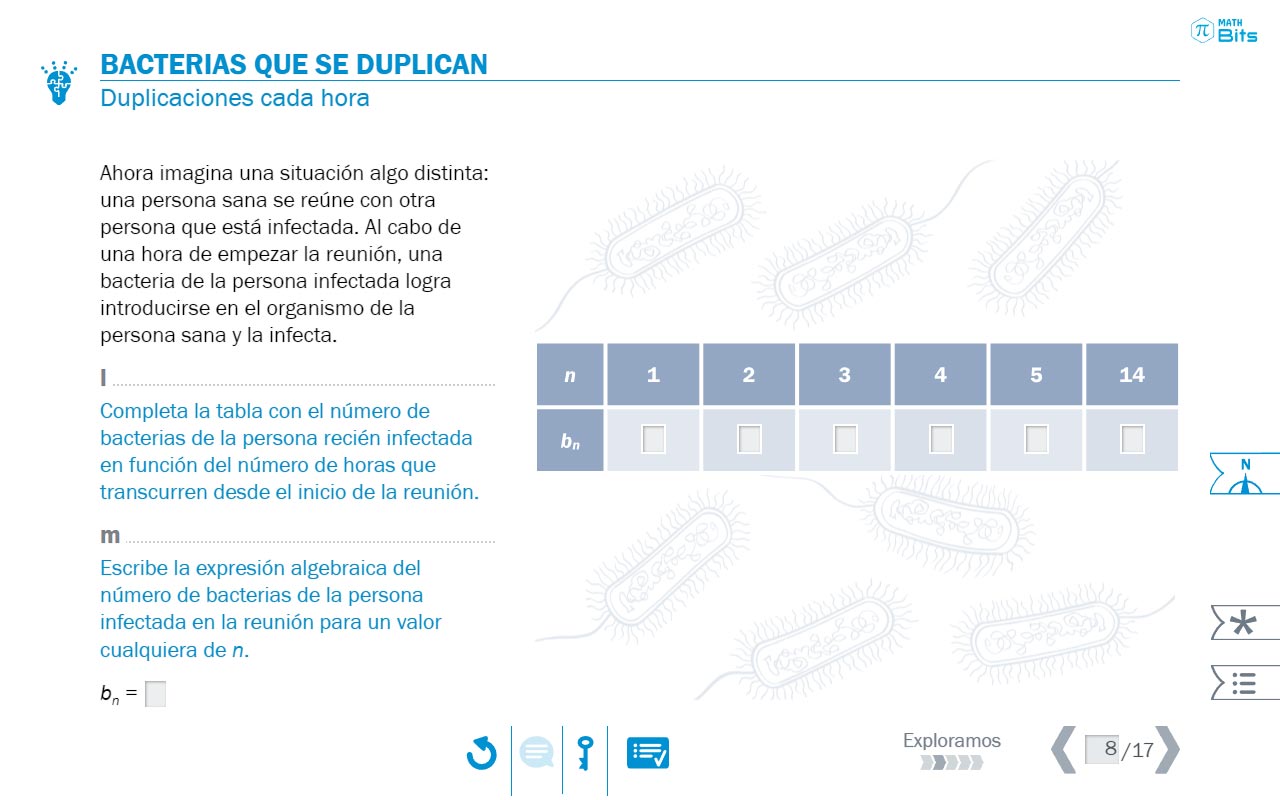
Esto se realiza dentro de un contexto similar al que se propone en el vídeo inicial de la unidad, relacionado con el crecimiento de una población de bacterias. En primer lugar, se comienza dejando que el alumnado utilice el registro gráfico para describir este crecimiento, instándole a fundamentar las razones detrás de su representación visual. Después, se propone averiguar la población en unos instantes determinados, lo que moviliza el registro tabular (o lista). Como el proceso es tedioso, a medida que se pretende averiguar la población en instantes avanzados de tiempo se hace necesario o deseable disponer de una fórmula. En este punto es cuando se introduce el lenguaje algebraico.
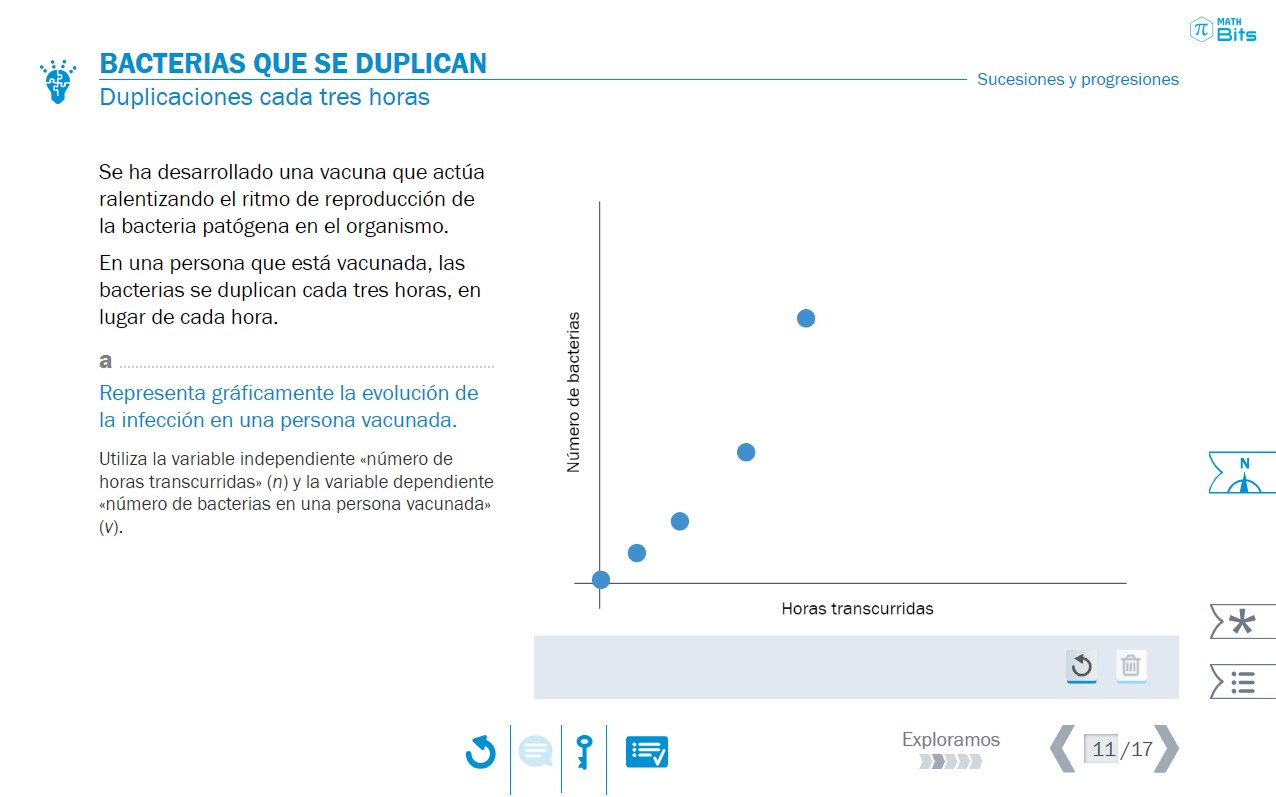
- El contexto del crecimiento de una colonia de bacterias permite introducir el lenguaje algebraico.
El hecho de introducir el registro algebraico no implica que nos olvidemos de la importancia de los demás registros, por lo que las actividades de exploración contemplan una articulación cuidadosa y una integración de lo aprendido anteriormente sobre el comportamiento de las sucesiones.
- Uso del registro gráfico para explorar el crecimiento de una sucesión numérica en un contexto realista.
Un problema interesante en torno a las sucesiones consiste en la suma de términos de una sucesión, lo que conecta con la idea de serie. En la unidad planteamos los números triangulares (los que expresan cardinales que se pueden representar en forma de triángulo equilátero) como contexto para abordar estas sumas.
- Los números triangulares ofrecen un contexto intramatemático excelente para explorar progresiones.
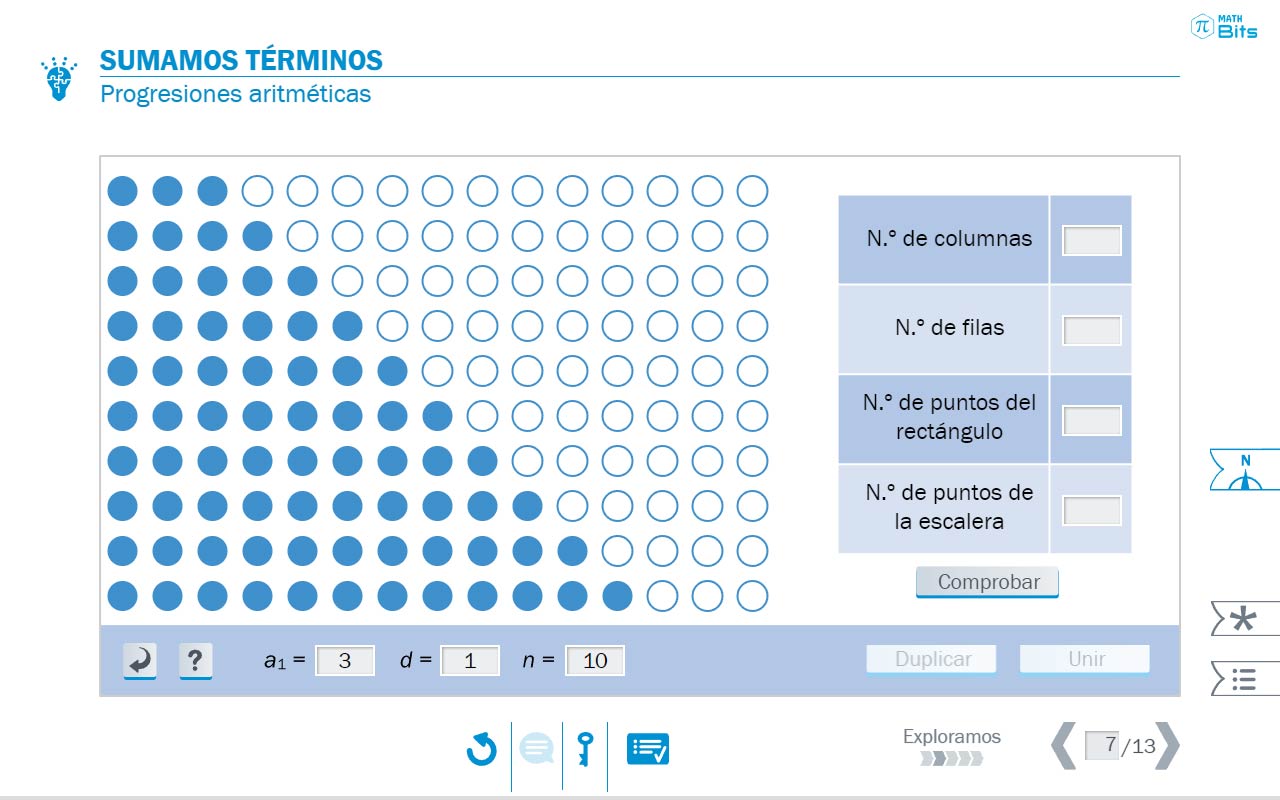
Los números triangulares dan paso a las progresiones aritméticas y geométricas, para las que se proporcionan recursos interactivos que facilitan, mediante soporte visual, los procesos de generalización que debe realizar el alumnado.
- Registro gráfico manipulativo para explorar la suma de los términos de una progresión aritmética.
¿Quieres saber más sobre las propuestas didácticas de Math Bits?
Si estás interesado en conocer una propuesta pedagógica altamente motivadora para tus estudiantes, basada en la investigación y el descubrimiento guiados, ponte en contacto con nosotros y te daremos acceso a las primeras unidades de muestra.
Referencias
Arnal-Palacián, M. (2019). Límite infinito de una sucesión: fenómenos que organiza. Tesis doctoral. Madrid, España: Universidad Complutense de Madrid.
Arnal-Palacián, M., Claros-Mellado, J., y Sánchez-Compaña, M. T. (2020). Infinite limit of sequences and its phenomenology. International Electronic Journal of Mathematics Education, 15(3), em0593.
Arnal-Palacián, M., Claros, F. J., Sánchez, M. T., y Baeza, M. A. (2017). Límite infinito de sucesiones y divergencia. Épsilon, 97, 7-22 .
Claros Mellado, F. J. (2010). Límite de una sucesión: fenómenos que organiza. Tesis doctoral. Granada, España: Universidad de Granada.
Cornu, B. (1991). Limits. En: D. Tall (Eds.), Advanced mathematical thinking (pp. 153-166). Dordrecht, Países Bajos: Kluwer.
Kidron, I., y Tall, D. (2015). The roles of visualization and symbolism in the potential and actual infinity of the limit process. Educational Studies in Mathematics, 88(2), 183-199.
Morales, A., Reyes, L. E., y Hernández, J.C. (2013). El límite al infinito. Análisis preliminar para la elaboración de una estrategia metodológica de su enseñanza-aprendizaje. Premisa, 15(3), 3-14.
Tall, D., y Schwarzenberger, R. L. (1978). Conflicts in the learning of real numbers and limits. Mathematics Teaching, 82, 44–49.
Thomas, M., de Freitas Druck, I., Huillet, D., Ju M. K., Nardi, E., Rasmussen. C., y Xie, J. (2014). Key mathematical concepts in the transition from secondary school to university. En: S. J. Cho (Eds.), Proceedings of the 12th International Congress on Mathematical Education (pp. 265–284). Nueva York, EE. UU.: Springer.














Deja una respuesta