Polinomios y funciones cuadráticas

22 de diciembre de 2023

Descubre y explora la esencia de la unidad Polinomios y funciones cuadráticas. Esta guía te ayudará a sacar más partido a los materiales de Math Bits.

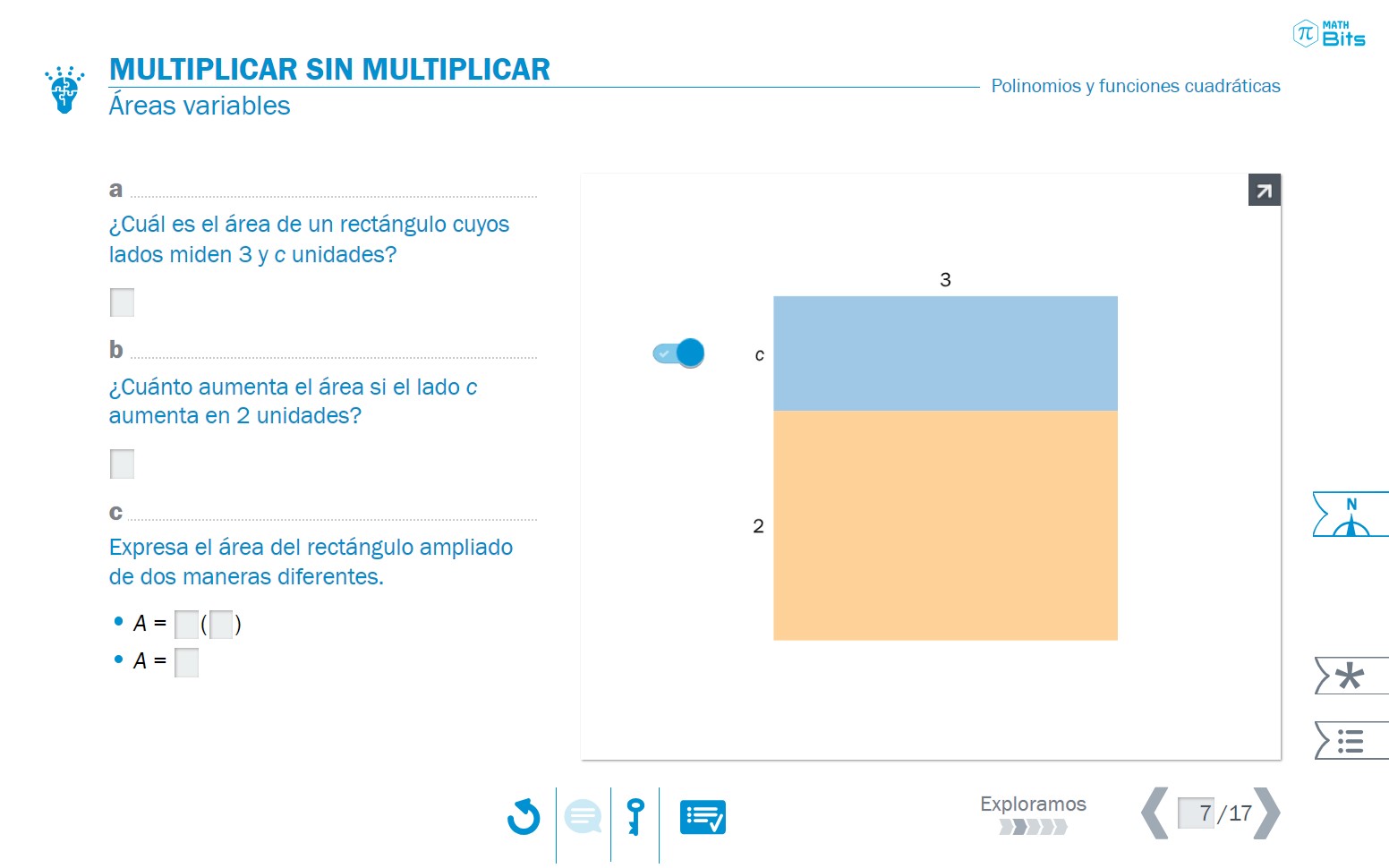
La unidad comienza recuperando el contexto intramatemático del cálculo de áreas de figuras rectangulares, en donde una de las dimensiones se aumenta o disminuye una longitud variable. El álgebra, de esta manera, nos ayuda a modelizar una situación que nos permitirá luego reflexionar sobre el propio lenguaje algebraico y la gestión de los signos. El hilo argumental arranca, por tanto, con el problema del producto de expresiones algebraicas. La reflexión sobre estas situaciones, una vez exploradas, permite abreviar las operaciones algebraicas que hay que efectuar, ya que se reconocen ciertos patrones (identidades notables).

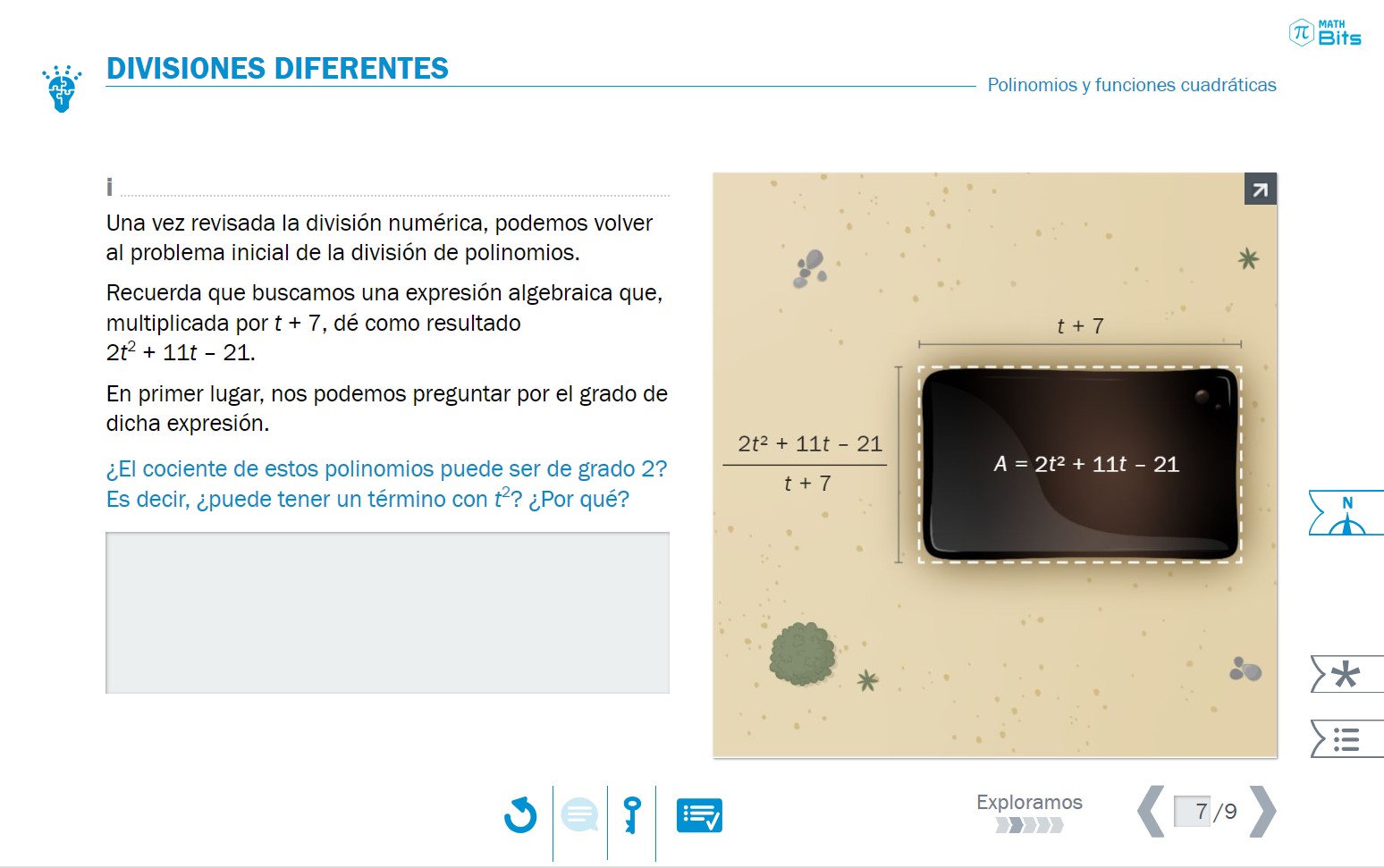
Dando la vuelta al contexto anterior, si lo que se pretende es averiguar la longitud de un lado del rectángulo siendo conocida su área, cobra sentido estudiar la división de expresiones algebraicas. Este es, habitualmente, un punto problemático para gran parte del alumnado. Por un lado, se suele abordar desde un punto de vista exclusivamente sintáctico, a partir de reglas que se han ido aprendiendo sin saber muy bien de dónde salen. Por otro lado, el docente de secundaria espera que el alumnado relacione el algoritmo de la división en caja para polinomios con la división en caja para naturales.

Con respecto a esto último, puede ocurrir que el alumnado no le haya encontrado sentido en su momento y que, por ejemplo, no sea consciente de que en cada fase hay una resta (recordemos que en el algoritmo tradicional, de manera muy poco fundamentada, la resta no se escribe). También puede pasar que el alumnado haya visto la división con otros algoritmos. Sin embargo, la cuestión principal es que el algoritmo de la división en caja para polinomios es muy diferente al de la división en caja para naturales. Por este motivo, aquí planteamos una división de números naturales con un algoritmo «extraño» que, a ojos del que conoce el tradicional, parecería incorrecto.

Una vez comprendido el algoritmo, la secuencia explora la misma idea pero con polinomios, mostrando de manera muy clara un trabajo matemático desde el punto de vista del pensamiento computacional. A partir de lo realizado con la multiplicación y la división, la secuencia se enfoca en la factorización de expresiones algebraicas.

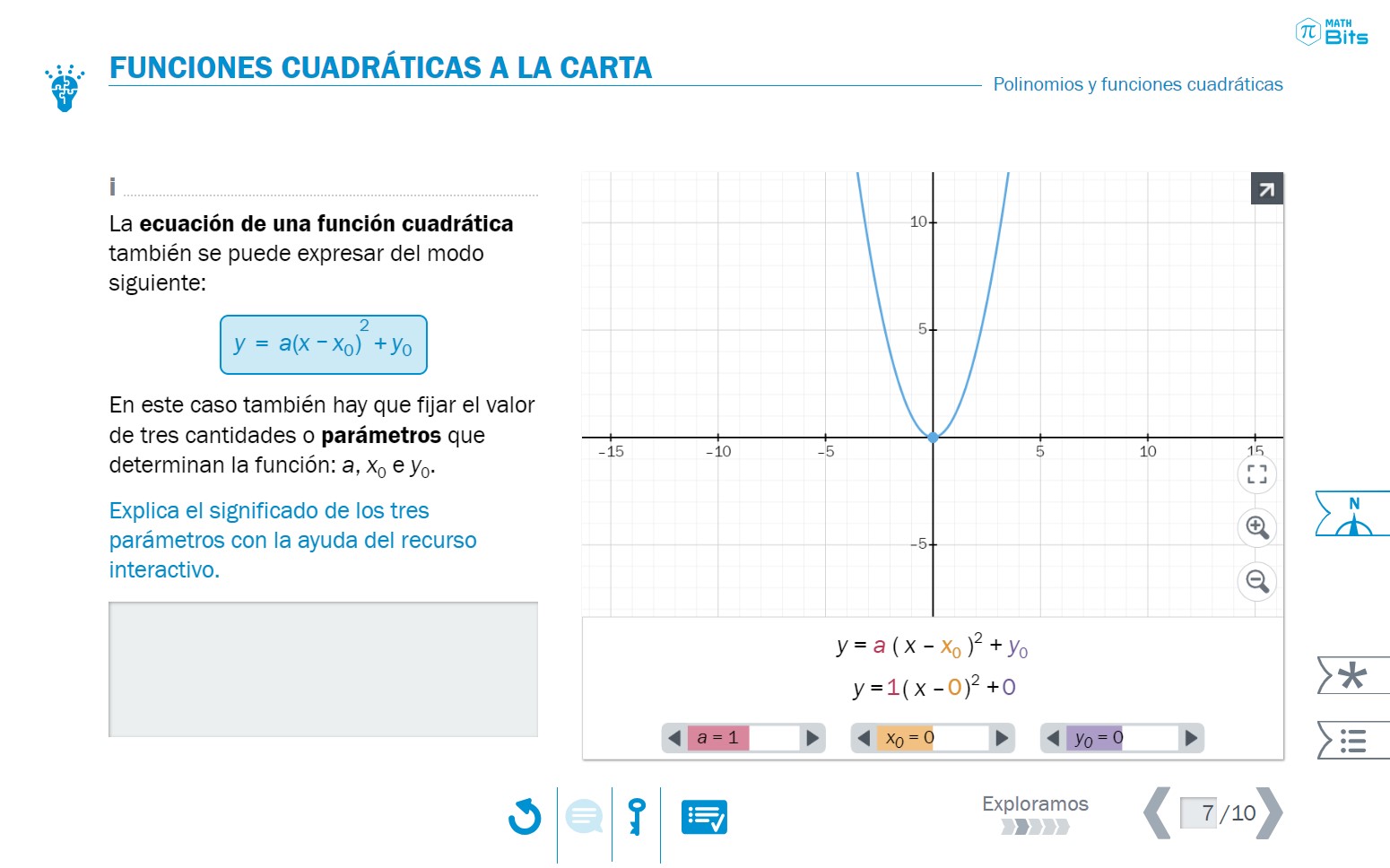
A continuación, se exploran las expresiones cuadráticas desde un enfoque funcional. De esta manera, una serie de interactivos virtuales permite estudiar esta familia de funciones y, en particular, el significado de los parámetros en cada forma de expresión. Es interesante que todo esto se presenta articulando los registros gráfico y algebraico, sin necesidad de operar en el algebraico en una primera instancia. Este modo de proceder sigue la filosofía presente en anteriores unidades sobre funciones y permite centrarse en los significados de los objetos matemáticos involucrados.

Finalmente, un problema que surge del trabajo anterior es la resolución de ecuaciones de segundo grado. La unidad incluye una serie de tareas en las que se explora cómo resolver este tipo de expresiones, reflexionando en cada caso en torno a diferentes técnicas y relacionándolas con el problema de la factorización. Cuando la ecuación es completa, se presenta la técnica conocida como «completado de cuadrados». Además, la exploración conjunta de las soluciones de una ecuación y los coeficientes de la variable permite reconocer patrones que facilitan averiguar las soluciones con «sentido algebraico» (esto constituye una aproximación a las relaciones de Cardano-Vieta).

¿Quieres saber más sobre las propuestas didácticas de Math Bits?

Si estás interesado en conocer una propuesta pedagógica altamente motivadora para tus estudiantes, basada en la investigación y el descubrimiento guiados, ponte en contacto con nosotros y te daremos acceso a las primeras unidades de muestra.

Referencias

Bednarz, N., Kieran, C., y Lee, L. (1996). Approaches to algebra. Dordrecht, Países Bajos: Kluwer Academic Publishers.

Drijvers, P. (Ed.). (2011). Secondary algebra education: Revisiting topics and themes and exploring the unknown. Rotterdam, Países Bajos: SensePublishers.

Kieran, C. (2020). Algebra teaching and learning. En Lerman, S.: Encyclopedia of mathematics education, 36-44. Dordrecht, Países Bajos: Springer Science y Business Media.

Leinhardt, G., Zaslavsky, O., y Stein, M. K. (1990). Functions, graphs, and graphing: Tasks, learning, and teaching. Review of Educational Research, 60(1), 1-64.

Molina, M. (2015). Concepciones del álgebra escolar. Granada, España: Dpto. Didáctica de la Matemática, Universidad de Granada.