Qué son los números reales
Explora la esencia y aplicaciones de los números reales en un recorrido desde los naturales hasta los irracionales. Esta guía te ayudará a profundizar en las matemáticas a través de los números reales.
19 de marzo de 2024

Evolución del Aprendizaje Numérico: De los Números Naturales a los Racionales
A lo largo de su trayectoria educativa, desde la etapa de educación infantil, los estudiantes entran en contacto con diferentes conjuntos numéricos y los exploran, a medida que van ampliándose al avanzar en su aprendizaje. De esta manera, el concepto de número se introduce a través del conjunto de los números naturales. El alumnado comienza a familiarizarse con ellos, aprende a contar, a reconocerlos y escribirlos, poniendo las primeras piedras fundamentales para la construcción de su pensamiento numérico. A continuación se introducen las situaciones aditivas (operaciones de suma y resta) y de paridad, y se inicia el estudio de las situaciones multiplicativas y cuestiones de divisibilidad. Todo ello permite el desarrollo de las habilidades de cálculo y una mayor comprensión de los patrones y propiedades de los números naturales.
En segundo y tercer ciclo de educación primaria comienzan a aparecer los números decimales y fracciones, y se amplía el conjunto numérico al de los números racionales (positivos). Esto proporciona una base para afrontar nuevos tipos de situaciones y problemas. En Math Bits se retoman estos fundamentos en la unidad Fracciones y decimales, donde se dota de sentido al número racional positivo mediante situaciones de medida de magnitudes continuas (longitud y área) y reparto. Estas situaciones constituyen razones de ser para este nuevo tipo de números, puesto que necesitamos el número racional para expresar cantidades de magnitud continuas. Recordemos que con este modelo de aprendizaje, que incide en el significado de la medida para introducir las fracciones, se persigue evitar los obstáculos asociados al modelo parte-todo habitual. Este puede impedir, por ejemplo, romper con las propiedades de los números naturales, si involucra un doble conteo.
El siguiente de los conjuntos numéricos en aparecer son los números enteros. En Math Bits esto se realiza en un entorno algebraico, dando los primeros pasos en el álgebra con literales a la vez que se construyen los enteros. De esta manera, se evitan los obstáculos que supone asociar el aprendizaje de los números enteros a modelos concretos, tales como ascensores, deudas o desplazamientos. Posteriormente, se termina de completar el conjunto de los racionales con los racionales negativos.
Matemáticas Vivas: Cómo los Números Reales Modelan Nuestro Mundo
En la unidad Los números reales terminamos de realizar la conexión definitiva entre la representación fraccionaria y la notación decimal de los números racionales. Esto permite revisitar propiedades como la densidad de este tipo de números y cómo se conecta esto con las diferentes representaciones. En primer lugar, recuperamos los repartos igualitarios, donde el número racional emerge tanto para expresar la acción en sí misma, el proceso, como la cantidad que recibe cada participante.
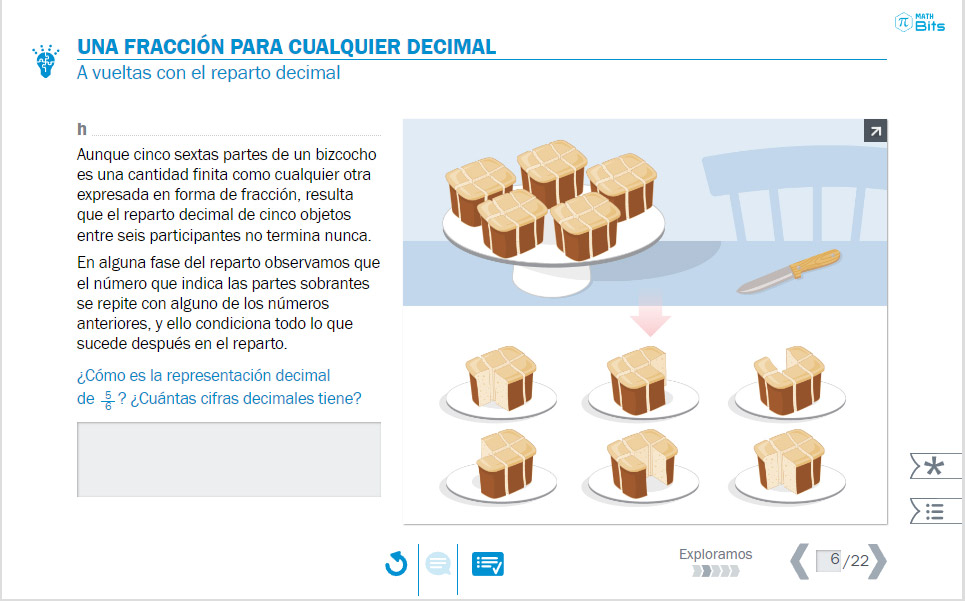
- Modelo de reparto para los números racionales.
Dependiendo del número de objetos a repartir y el número de participantes, se obtiene un tipo de representación decimal u otro.
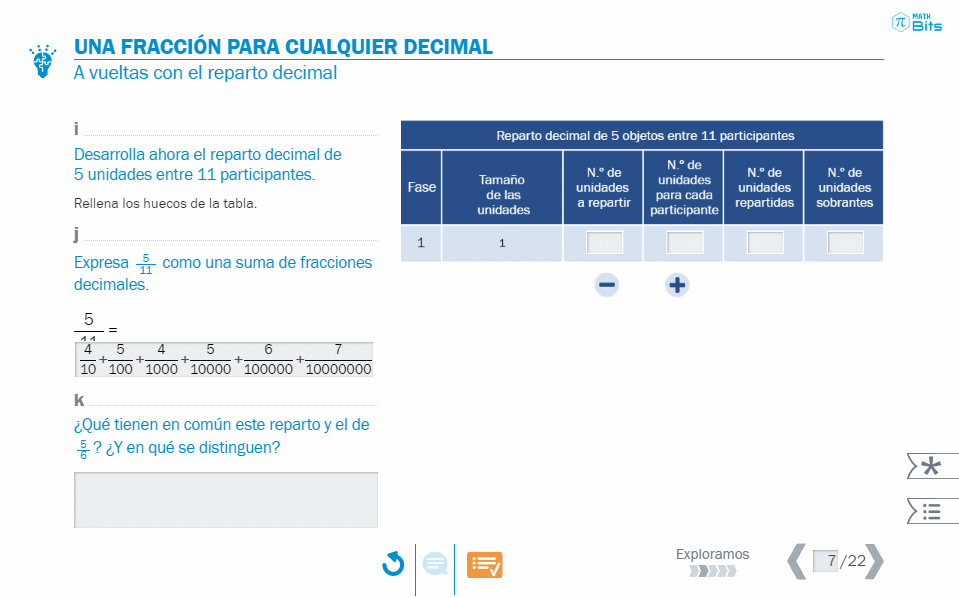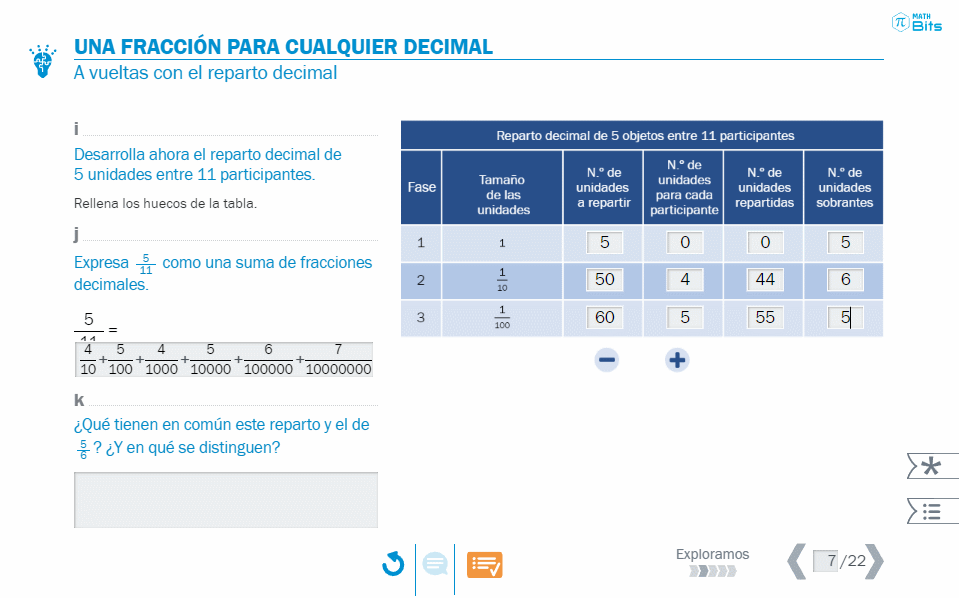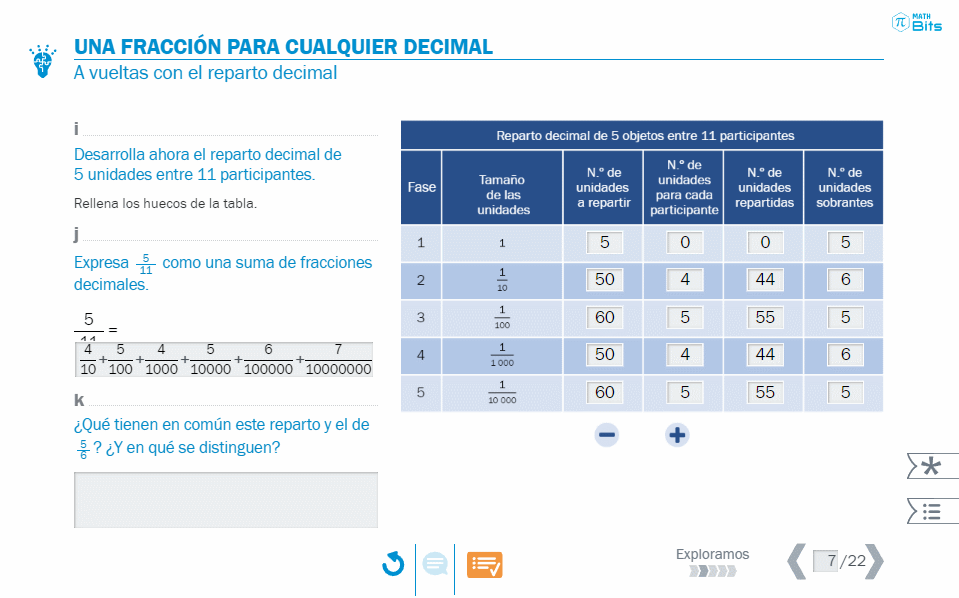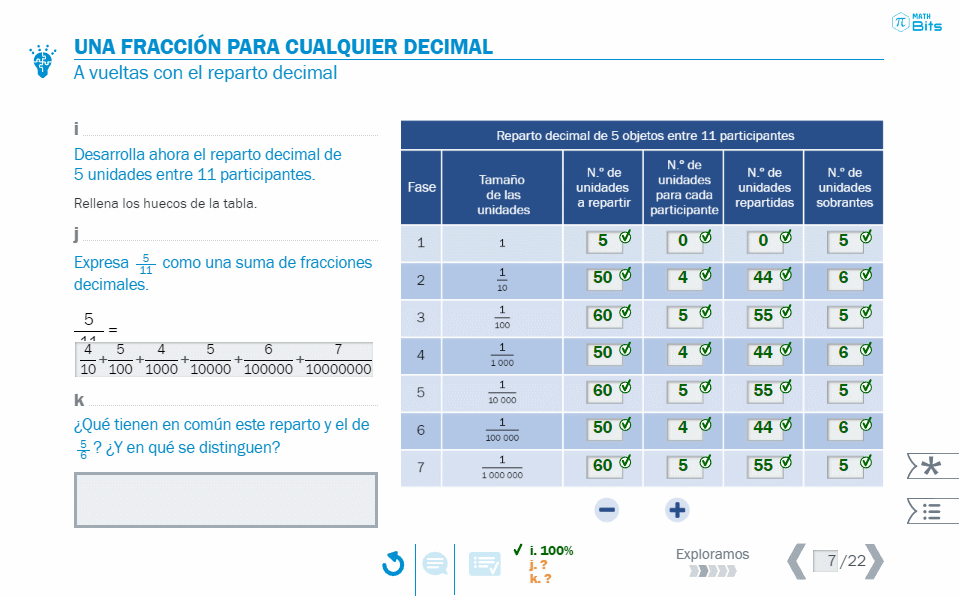
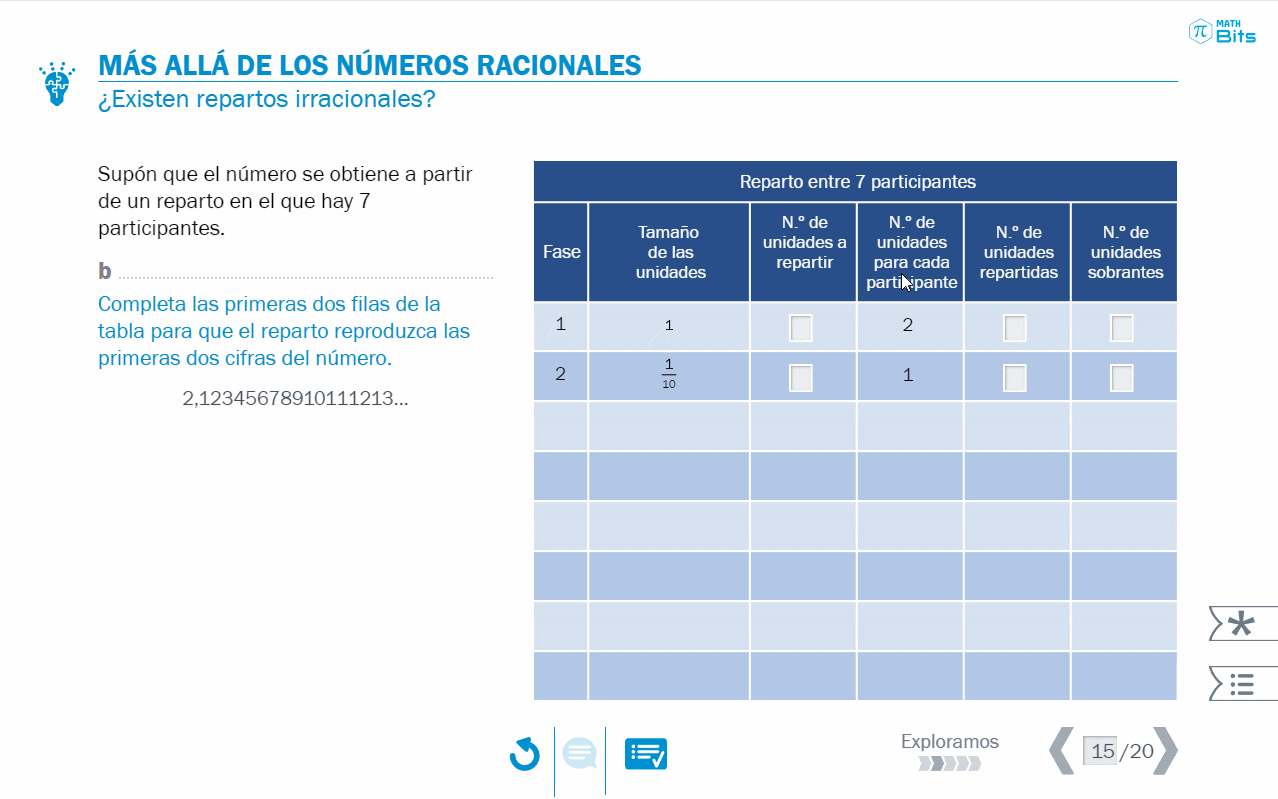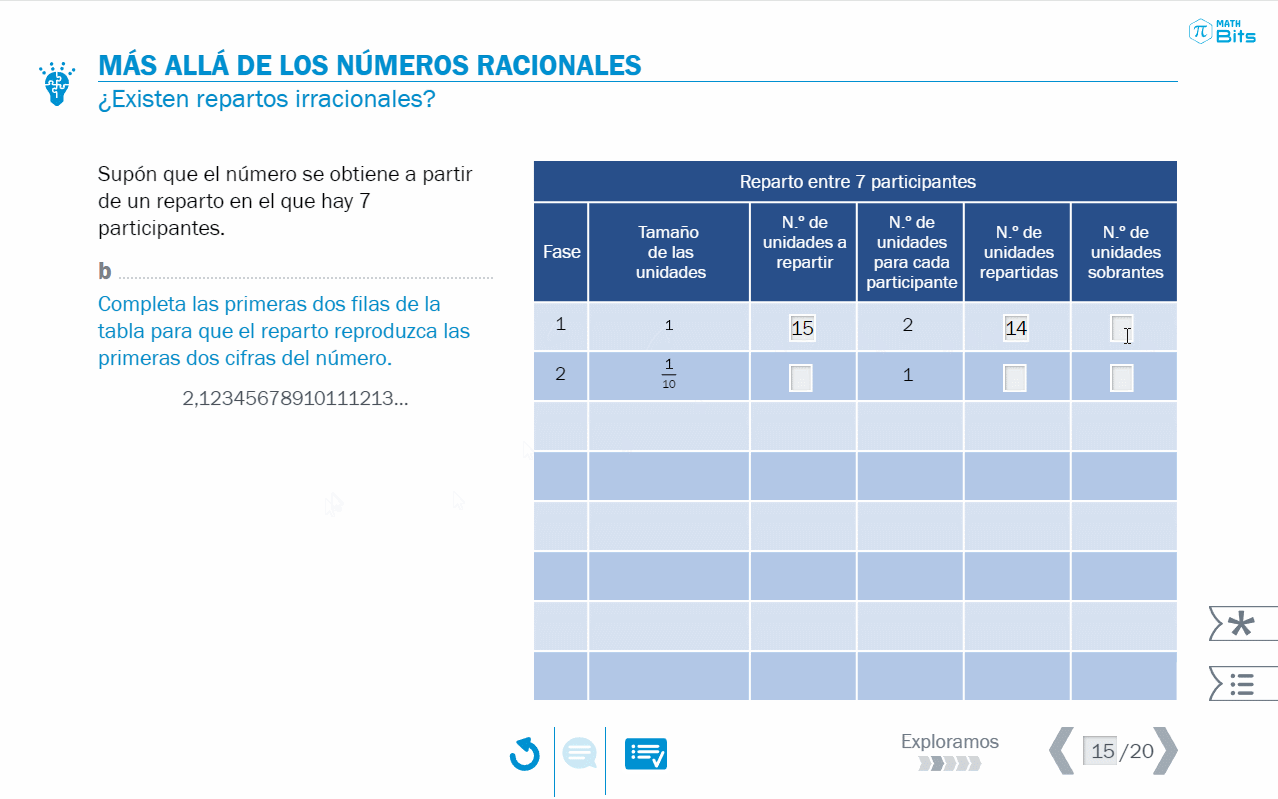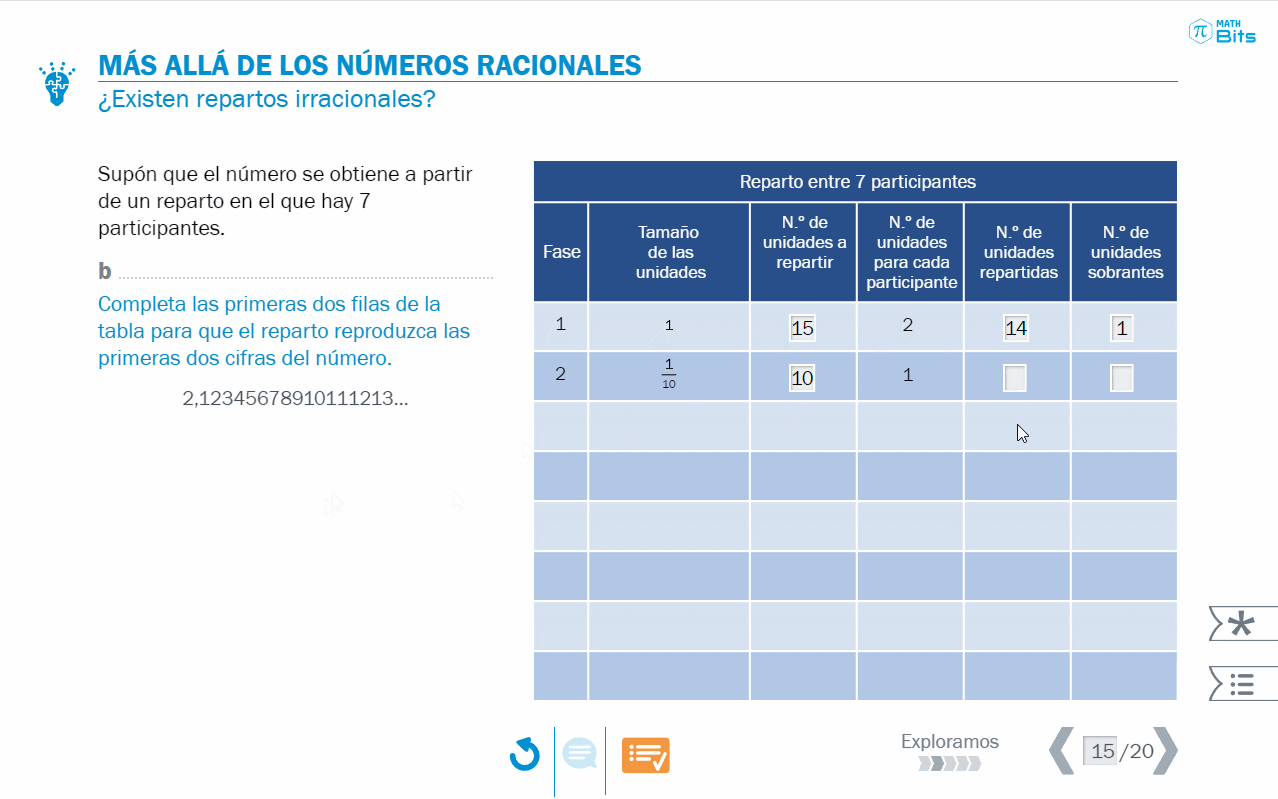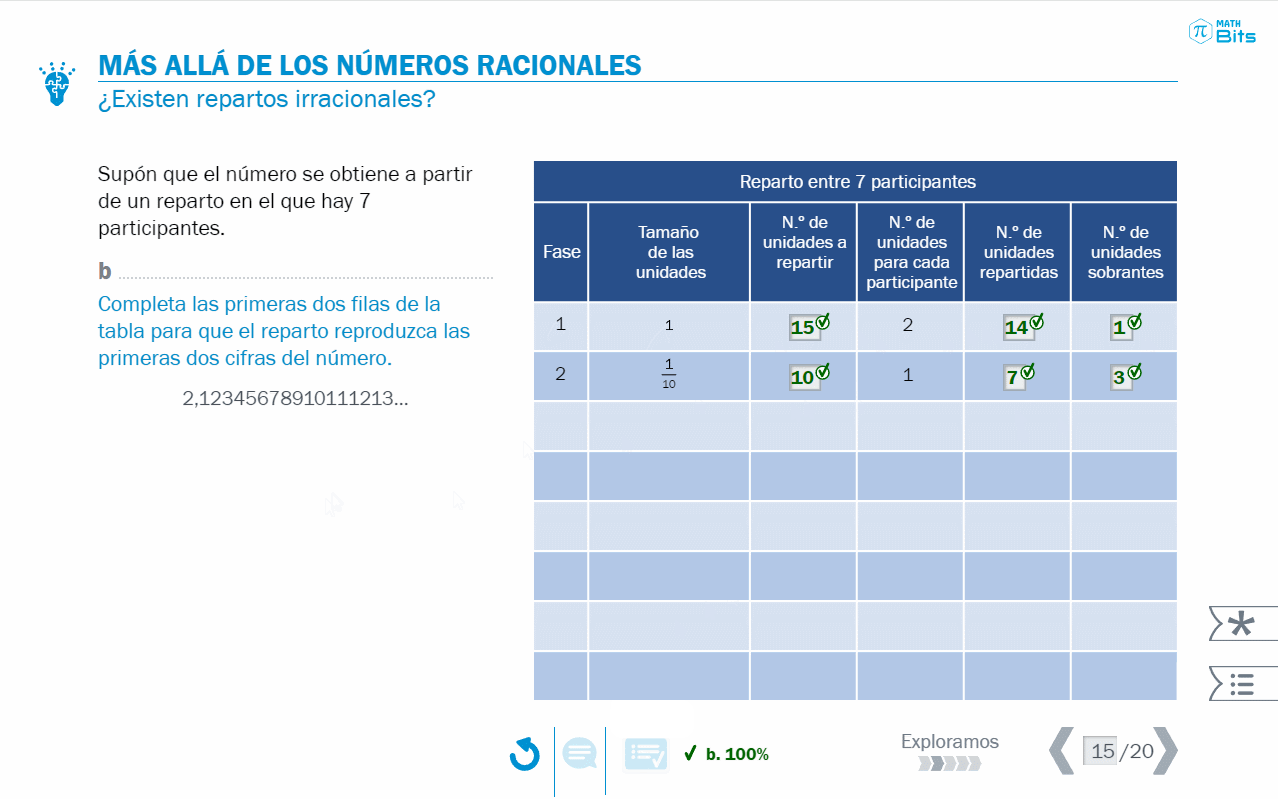
- Tabla donde se desgrana el proceso de reparto que da lugar a una representación polinómica decimal.
Como colofón a esta primera parte y para cerrar la conexión entre la representación decimal y la fracción, se plantea el problema de averiguar las condiciones iniciales de un reparto (número de objetos a repartir y número de participantes), dada la cantidad que recibe cada participante, expresada en notación decimal. En el fondo, se trata de averiguar la fracción generatriz de un número decimal. La reflexión más interesante que surge en este momento es que los números que admiten una representación decimal finita también admiten otra infinita, disminuyendo la última cifra significativa y añadiendo una «cola» infinita de nueves.
- Uso del lenguaje algebraico para explorar el reparto decimal de a objetos entre b participantes.
Del Racional al Número Real: Descubriendo los Números Infinitos y No Repetitivos
A continuación, estudiaremos las condiciones que deben darse para que la representación decimal de la cantidad que recibe un participante en uno de estos repartos sea infinita (¡no así la cantidad que recibe!). En otras palabras, lo que estamos explorando es cuándo una fracción irreducible da lugar a una representación decimal periódica.
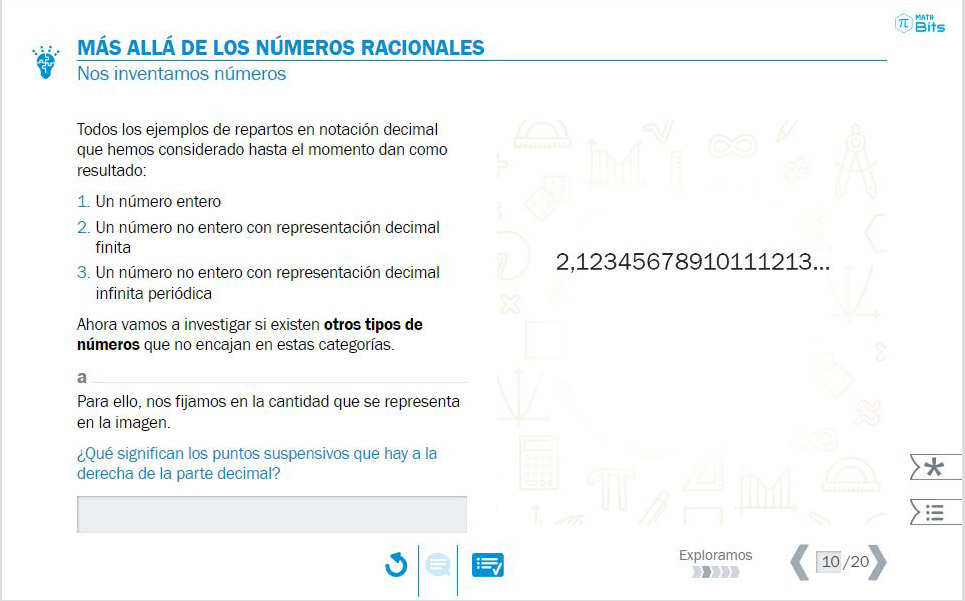
Hecho esto, nos adentramos —ahora sí— en el mundo de los números reales, recuperando los procesos de medida y reparto que dieron lugar a la necesidad de los racionales y a sus diferentes representaciones. Ahora bien, para intuir que hay números especiales distintos a los racionales basta con observar que podemos inventarnos números cuya representación decimal es infinita y no se repite.
- Podemos inventarnos un número como este fácilmente. ¿Será racional?
Con este tipo de números ocurre que, al considerarlos como la representación decimal de un hipotético reparto, se observa que es imposible reconstruir las fases de distribución, pues en algún momento los restos deberían repetirse. Y eso es algo que no ocurre en este caso.
- Las tablas que permiten modelizar el reparto abren la puerta a explorar qué ocurre si no se repite ninguna cantidad de ninguna fase.
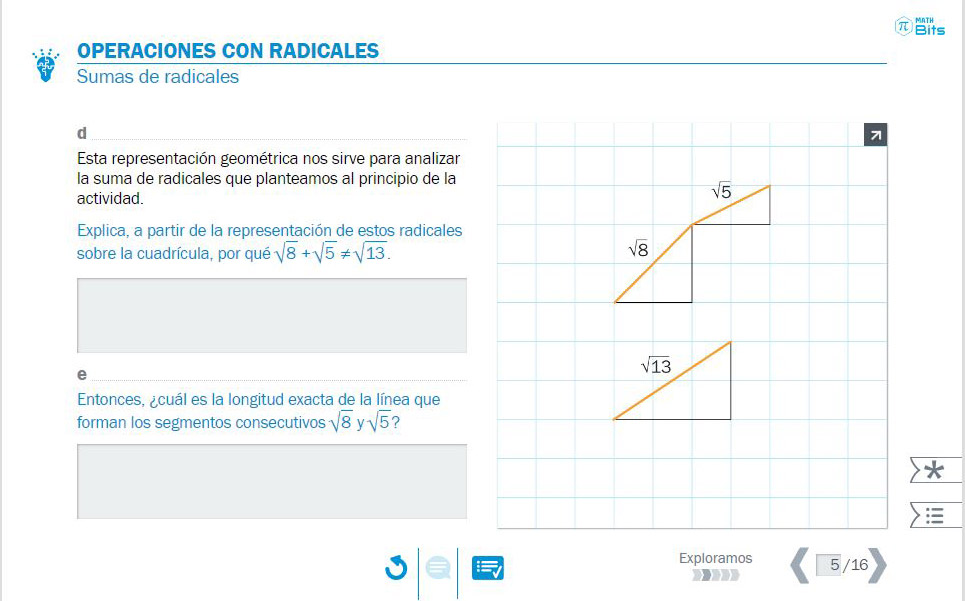
Pero los números reales también aparecen en contextos de medida. Sin ir más lejos, hay cantidades de magnitud (longitudes, por ejemplo) que son inconmensurables. Así, no podemos subdividir el lado de un cuadrado de tal manera que podamos medir de forma exacta la diagonal con esas subunidades. En Math Bits profundizamos en esta idea para ilustrar qué significa el signo radical y cómo así podemos expresar ciertas longitudes. No solo eso, sino que mediante el trabajo con geoplanos se facilita el aprendizaje de cómo operar con ellos.
- Cuadrícula que permite apreciar que existen medidas de longitudes que no son racionales, así como explorar la agregación o sustracción de estas cantidades de magnitud.
Reflexiones sobre Pi y Más: Entendiendo los Números Especiales y sus Propiedades
En realidad, los números reales son viejos conocidos para el alumnado, como el número pi, el cual les lleva acompañando desde la educación primaria. Ahora bien, ¿qué es pi? Dejando a un lado una demostración rigurosa de su irracionalidad, ¿se ha conjeturado algo sobre ella? ¿Se ha reflexionado que es algo más que 3,14? ¿Que estamos ante un representante de un tipo de números «especiales»? Lo mismo ocurre con las raíces que no son exactas. Es el momento de realizar estas y otras reflexiones, que nos permitirán aprender sobre este tipo de números y sus propiedades. Igualmente, con todos los conjuntos sobre la mesa (naturales, racionales, enteros y reales), aprovecharemos la ocasión para formalizarlos al nivel correspondiente. Observaremos cómo se mantienen algunas propiedades con respecto al conjunto de partida y cómo cambian otras, así como los efectos y significados de las operaciones que se pueden realizar con ellos.
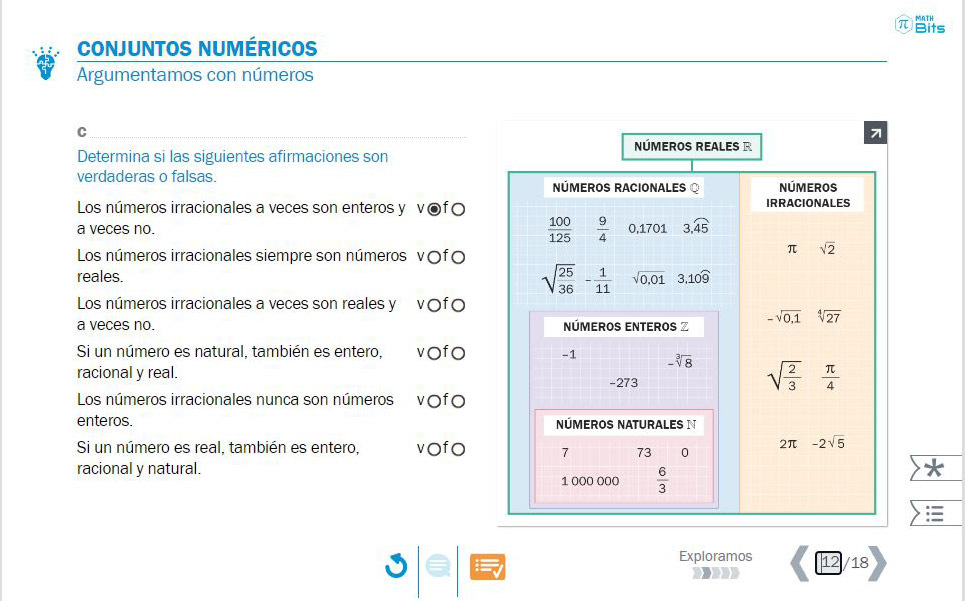
Para llevar a cabo estas reflexiones sobre los conjuntos numéricos se hace indispensable un trabajo previo sobre el lenguaje. Es necesario, por tanto, abandonar por un momento la cuestión puramente matemática y centrarse en desarrollar habilidades para argumentar la veracidad o falsedad de enunciados. En concreto, los que usan determinados cuantificadores (todos, alguno, ninguno) y calificadores modales (siempre, a veces, probablemente, depende). Entonces ya podremos razonar sobre los números y sus propiedades.
- Actividad que pone sobre la mesa diferentes proposiciones que se pueden formular en torno a los diversos conjuntos numéricos.
En definitiva, el acercamiento a los diferentes conjuntos numéricos y la introducción de los números reales exige una serie de reflexiones profundas que vienen a condensar una trayectoria que comenzó en educación infantil con ese primer contacto con los números naturales. No es algo que deba trivializarse con meros ejercicios de clasificación, obviando los razonamientos que crean esas clases.
¿Quieres saber más sobre las propuestas didácticas de Math Bits?
Si estás interesado en conocer una propuesta pedagógica altamente motivadora para tus estudiantes, basada en la investigación y el descubrimiento guiados, ponte en contacto con nosotros y te daremos acceso a las primeras unidades de muestra.
Referencias
Gairín, J. M., y Sancho, J. (2002). Números y algoritmos. Madrid, España: Síntesis.














Deja una respuesta