
La proporcionalidad representa la culminación de la aritmética, por lo que quizás constituye su parte más compleja y comporta numerosas dificultades de comprensión. Más allá de limitarse al estudio de técnicas para resolver un tipo concreto de ejercicios, su aprendizaje debería ir orientado al desarrollo del pensamiento proporcional. De hecho, la literatura especializada arroja evidencias de que un aprendizaje mecanicista fomenta la llamada «ilusión de linealidad», la cual conduce a los estudiantes a abordar problemas que no implican relaciones de proporcionalidad como si así lo hicieran.
Por ello, esta unidad incide especialmente en el razonamiento en torno a la idea de razón y cómo esta surge en situaciones variadas; no solo en las que hay que encontrar un valor desconocido, sino también en situaciones de comparación. Así, resulta fundamental un buen trabajo previo con el concepto de magnitud y, a continuación, una reflexión sobre las condiciones de regularidad, esto es, las condiciones que deben darse para poder hablar de proporcionalidad directa entre magnitudes.
Algunos de los recursos destacados que encontraréis en la unidad ‘Proporcionalidad’ de Math Bits:
- ¿Qué condición debe cumplir una relación entre magnitudes para poder hablar de proporcionalidad directa?
- ¿Qué condición debe cumplir una relación entre magnitudes para poder hablar de proporcionalidad directa?
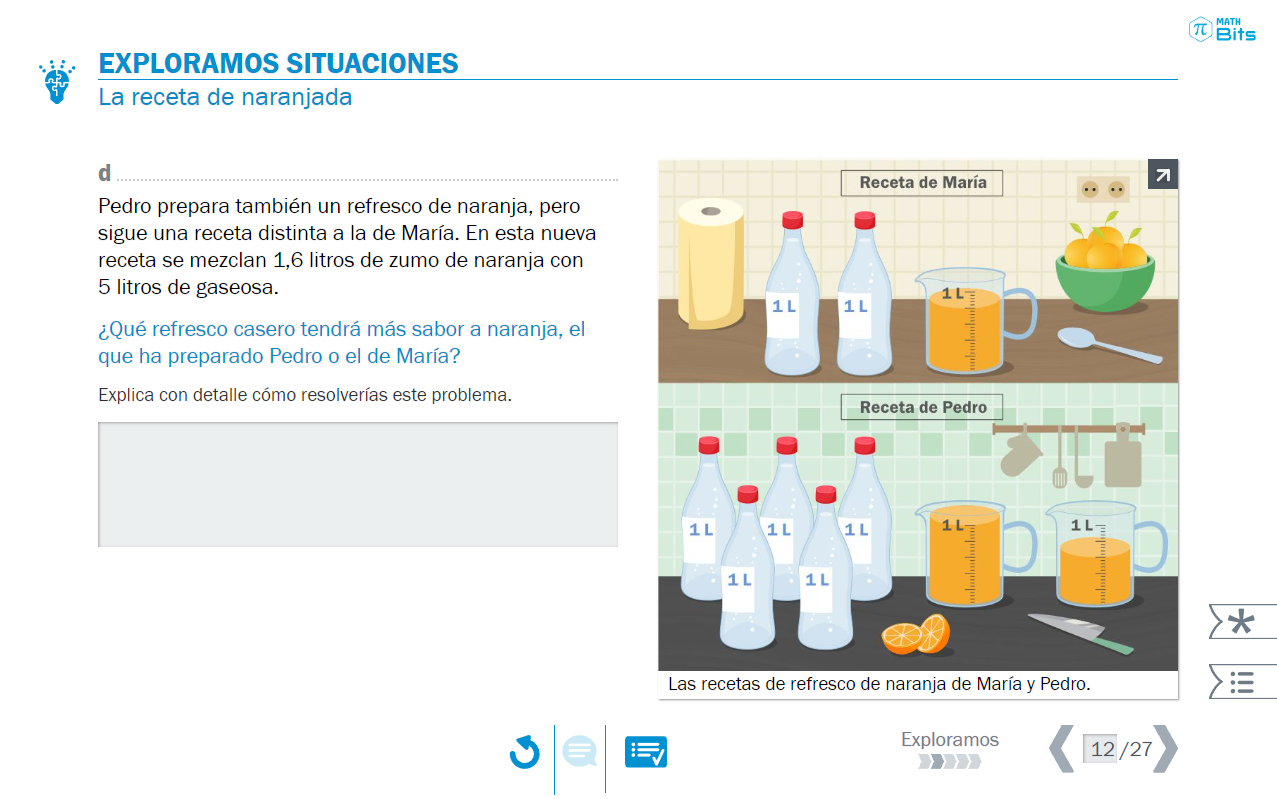
- La razón entre magnitudes da lugar a una nueva magnitud. En la imagen, una situación de comparación en la que surge la idea de “intensidad de sabor”.
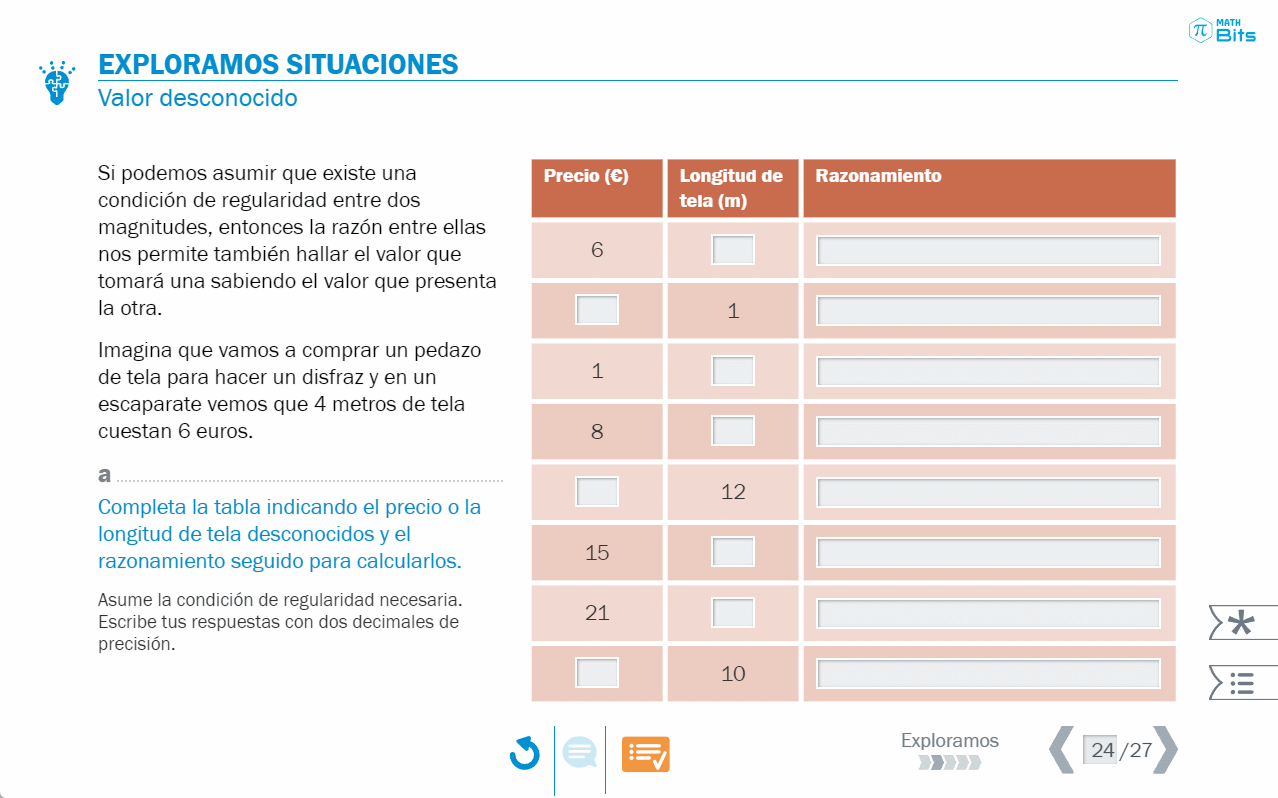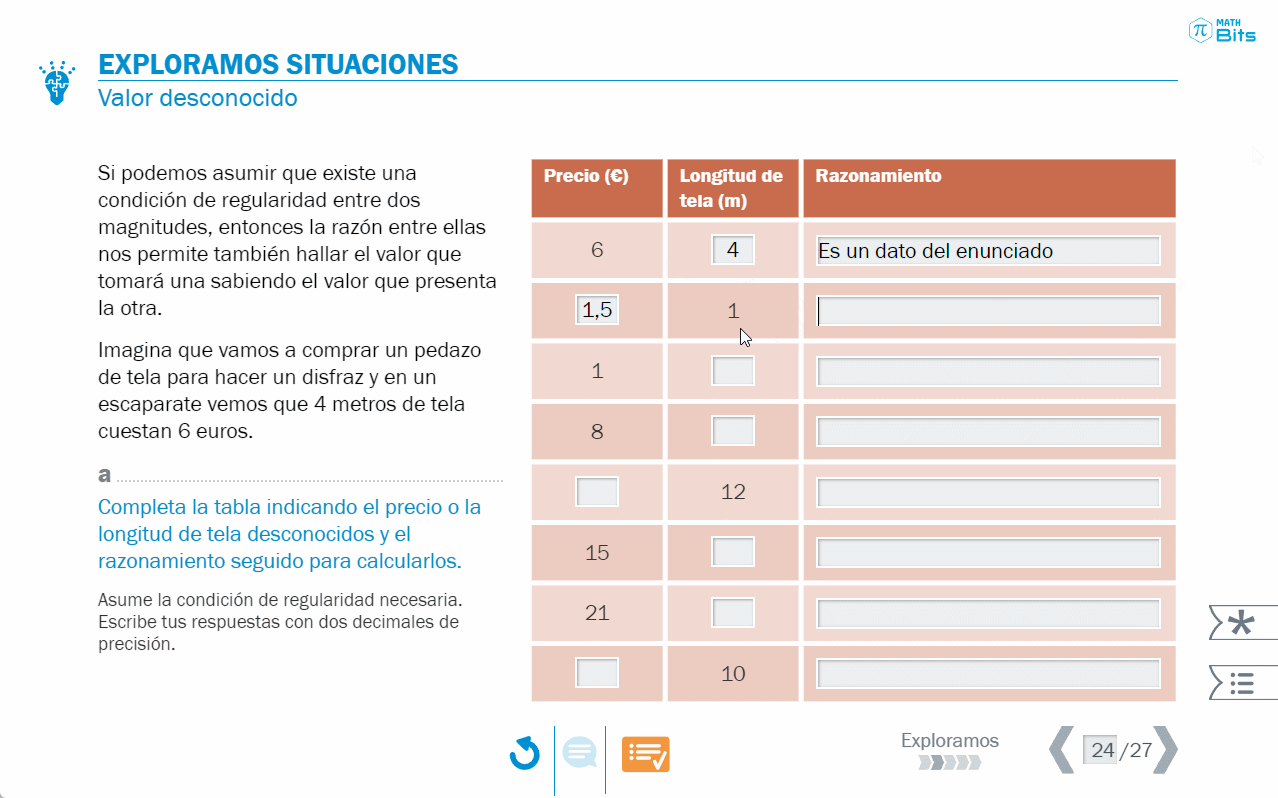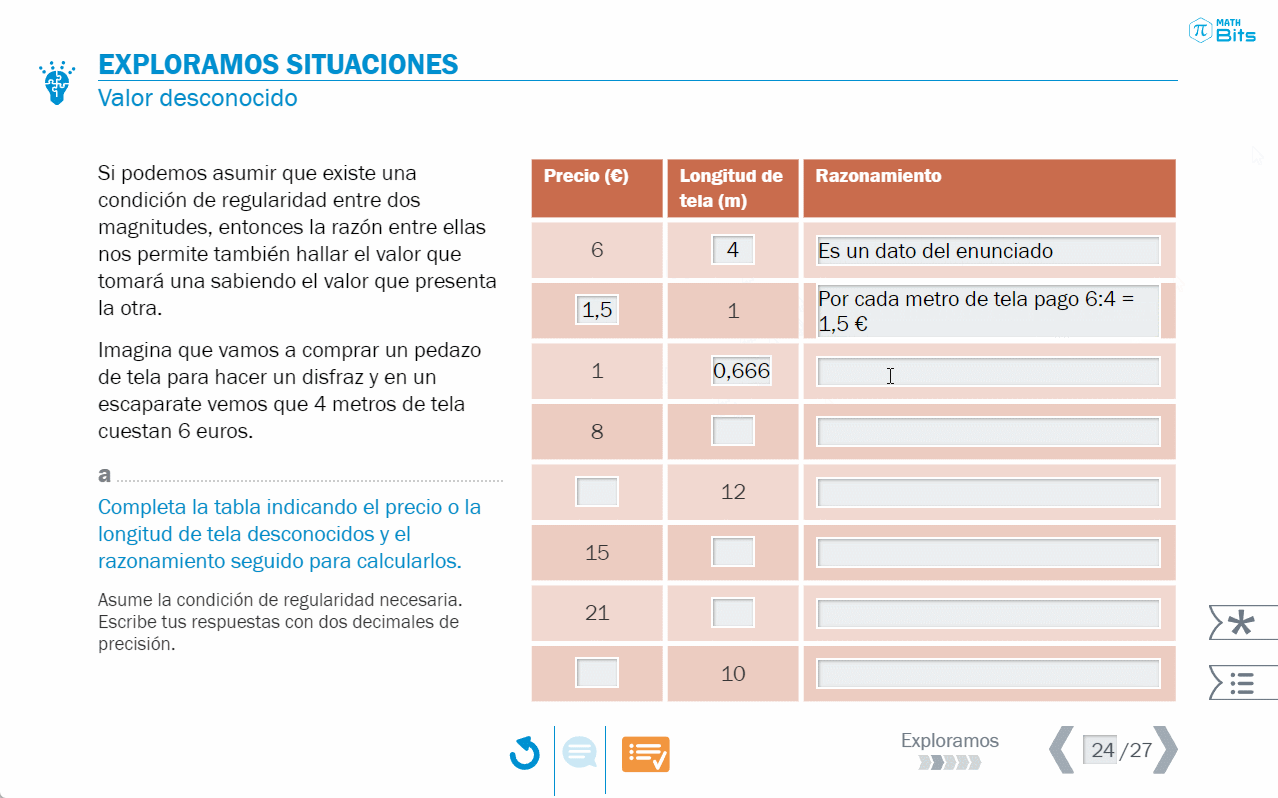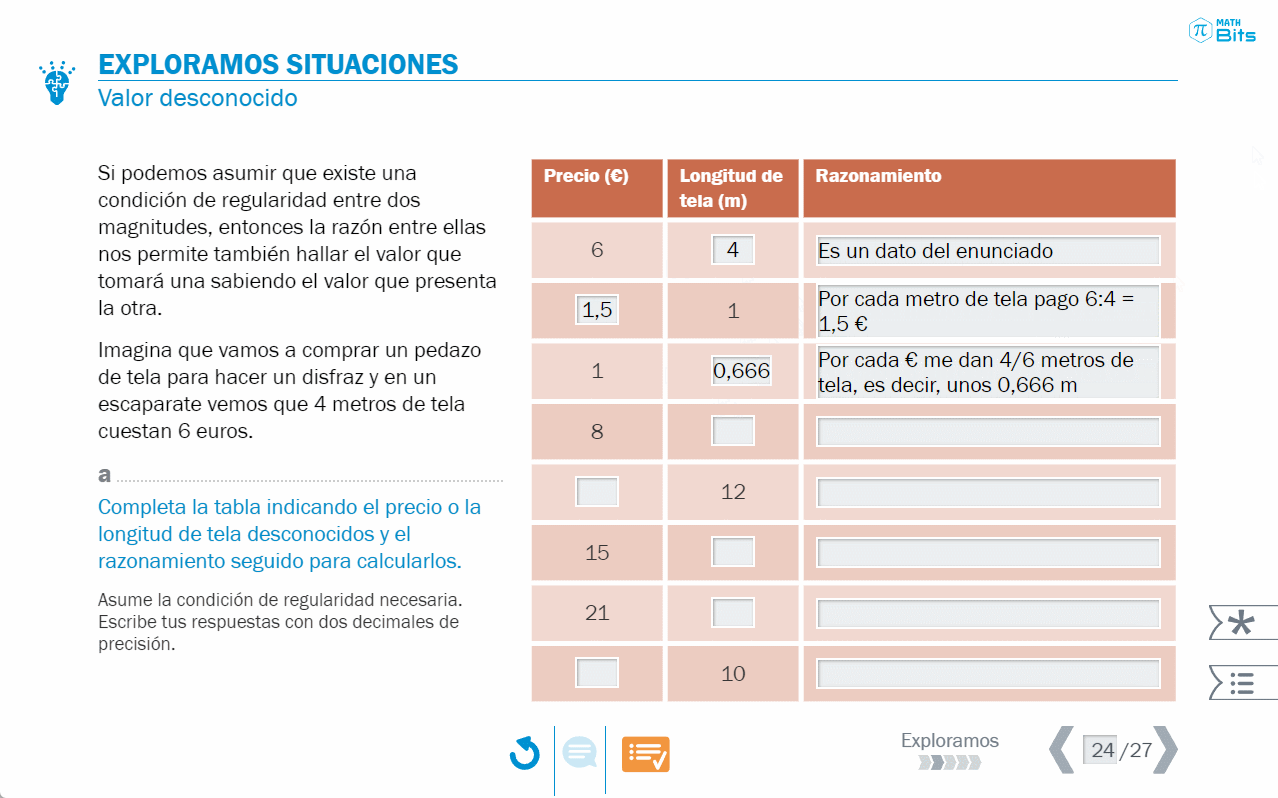
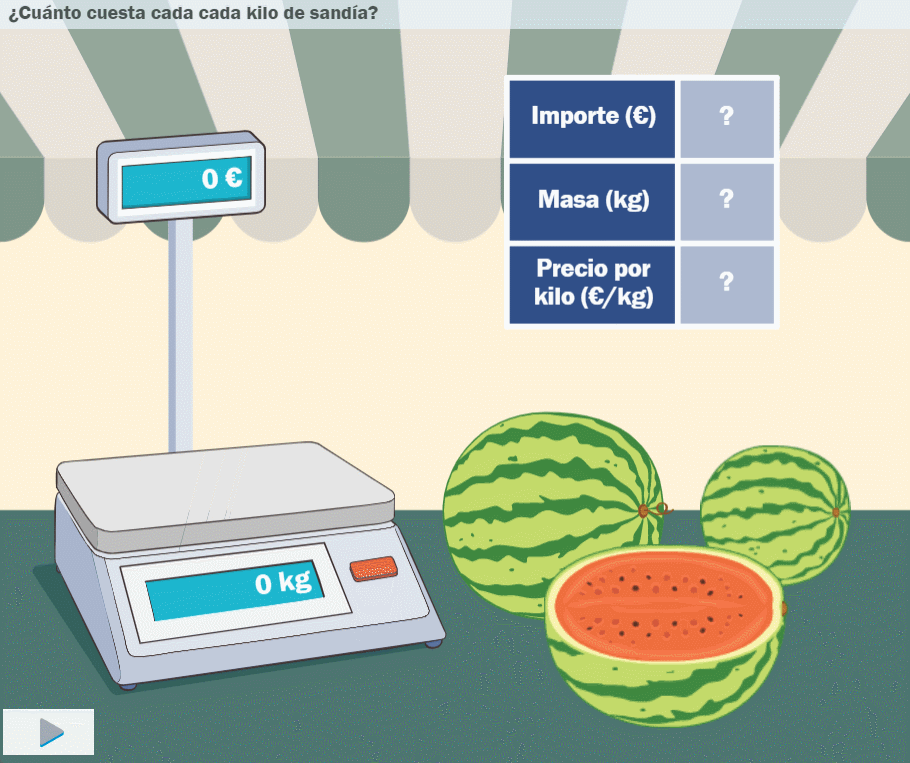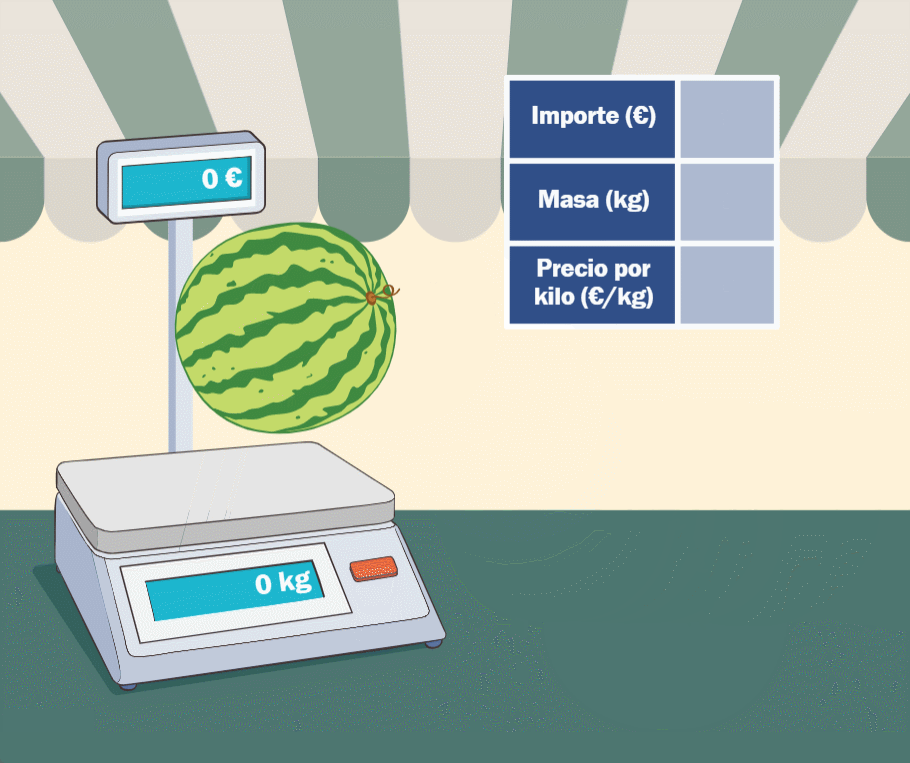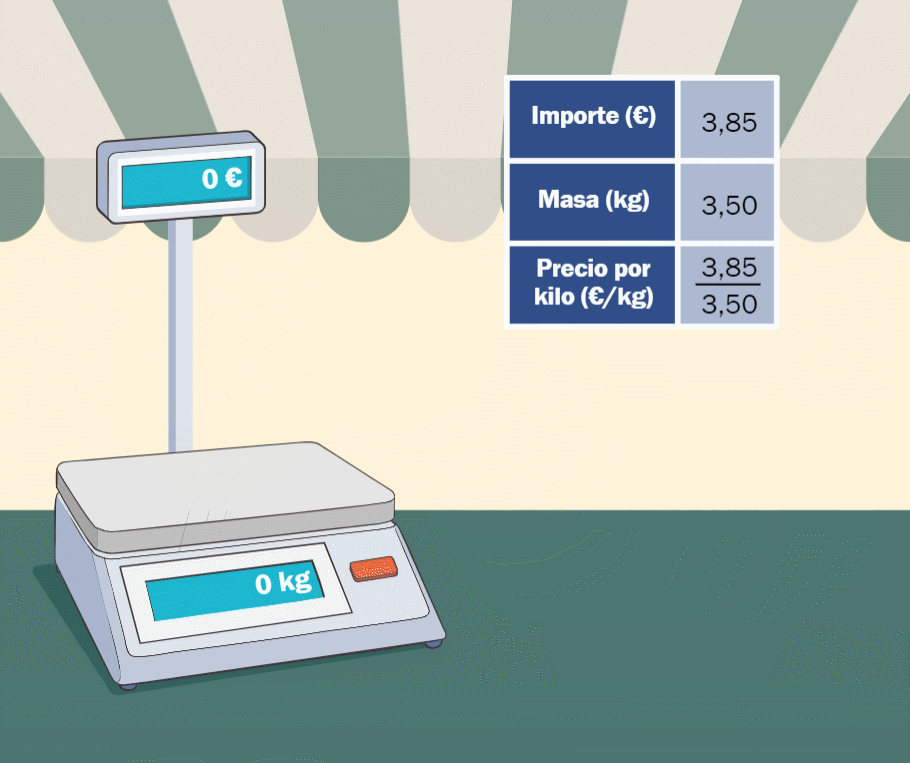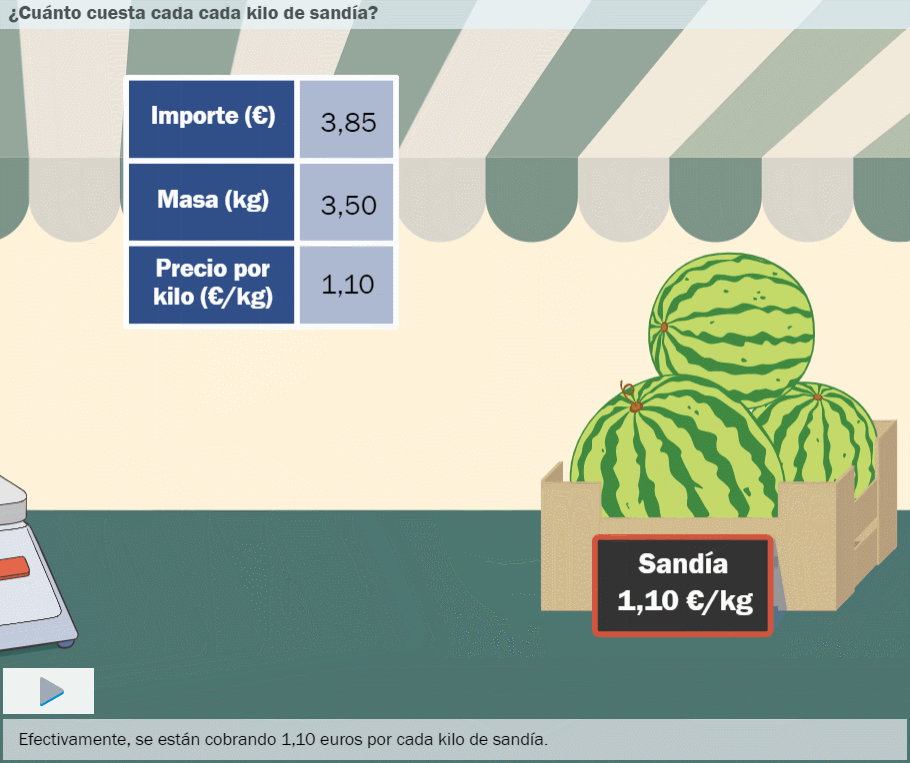
- Situaciones de proporcionalidad directa en las que hay que averiguar un valor desconocido. La estructura numérica está diseñada para desarrollar el razonamiento aritmético a partir de la idea de razón.
- ¿Qué condición debe cumplir una relación entre magnitudes para poder hablar de proporcionalidad directa?
- El porcentaje es mucho más de lo que parece. Expresan una relación de proporcionalidad entre dos cantidades de magnitud.
















Deja una respuesta