En esta unidad se encuentran dos caminos que recorren la propuesta de Math Bits desde el primer curso de educación secundaria. Uno, el que construye el número racional positivo a partir del significado de medida y de reparto. Otro, el que introduce los números enteros en un entorno algebraico. De esta manera, uno de los problemas didácticos que abordamos aquí es el de completar los números racionales con los números racionales negativos. A través de la resolución de problemas, como veremos, el alumnado será consciente de que los números racionales son algo más que una forma de expresar cantidades de magnitud, un conjunto numérico en sí mismo. La unidad se completa con los sistemas de ecuaciones, a los que nos acercaremos desde una perspectiva funcional; es decir, privilegiando la idea de letra como variable, y tratando de conectar el discurso aritmético con el algebraico.

Para introducir los racionales «con signo» es necesario promover reflexiones similares a las que se llevaron a cabo con los enteros. Por eso, la primera lección, «Fracciones y decimales con signo», propone emplear expresiones algebraicas que permiten modelizar situaciones en las que la cantidad desconocida puede ser un incremento, ganancia o aumento, y también un decremento, pérdida o disminución. Por lo tanto, las expresiones algebraicas que van a aparecer juegan con la estructura aditiva de los números racionales. Se trata de dar sentido a los sumandos y sustraendos aislados, primero como cantidades positivas y negativas para, finalmente, poder reflexionar acerca de que estamos ante un tipo de números conocido como números racionales. Al mismo tiempo, y como parte de este proceso de construcción de significado, se proporcionan situaciones para apreciar el uso de los signos cuando usamos notación fraccionaria.

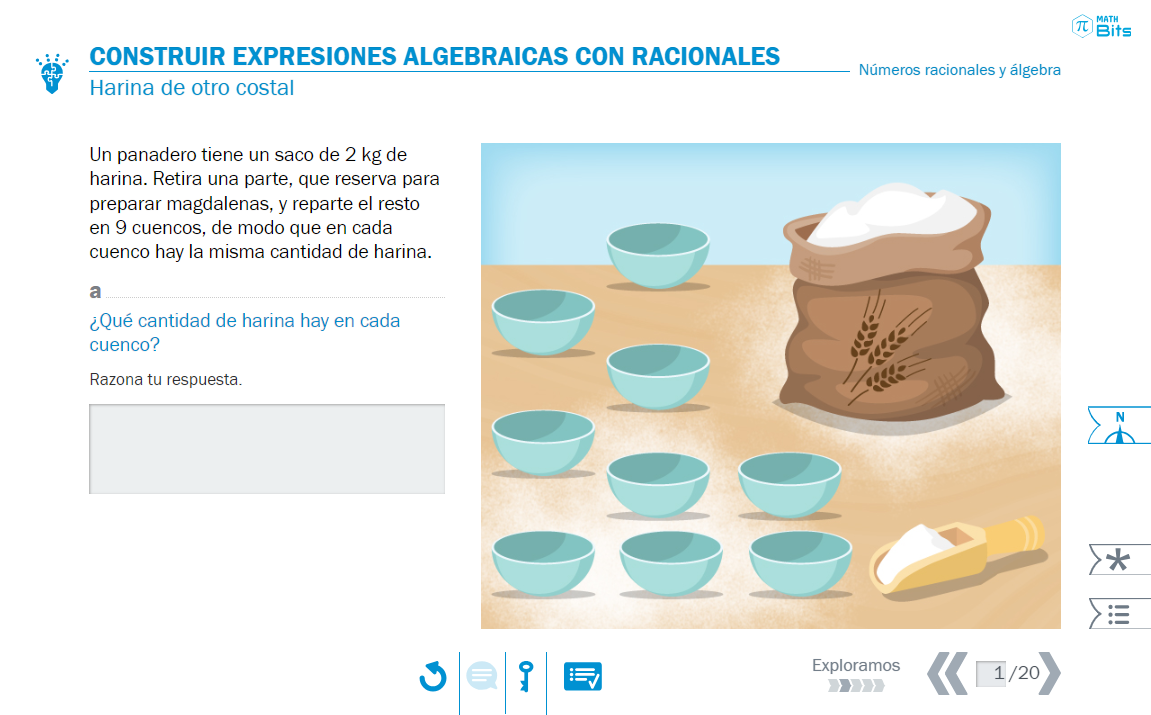
A continuación, una nueva situación permitirá construir expresiones algebraicas más complejas:

En particular, conviene observar la conexión de esta situación con el significado como reparto de los números racionales. El alumnado podrá apreciar la equivalencia de estas tres expresiones:

En efecto, cada una de estas expresiones conecta con la interpretación del cociente, bien como un reparto entre 9 participantes o como una modificación de una cantidad de magnitud (como la novena parte de una cantidad). Es importante ser consciente de este juego de representaciones, pues transformar el cociente en un producto permitirá manejar mejor las expresiones algebraicas y extender las técnicas conocidas para racionales positivos y enteros.

En esta línea se propone otra situación para reflexionar sobre la diferencia de expresiones algebraicas, así como para abordar la generalización de técnicas ya conocidas por el alumnado, en el ámbito de la aritmética del racional positivo. La situación es la comparación de las alturas de dos rectángulos con la misma área, habiéndose obtenido uno de ellos variando la longitud del otro lado (la base).

De esta manera, la expresión de la diferencia es:

Y, como podemos apreciar, se trata de extender la idea de buscar un denominador común. En ese sentido, la secuencia de tareas aporta el andamiaje necesario para que el alumnado llegue a la generalización.

A continuación, la unidad se enfoca en el álgebra y la resolución de problemas. No es que hasta ahora se haya evitado esto último, pero ahora queremos profundizar en la relación del álgebra con el proceso de resolución de problemas. Así, en el exploramos «Comprender y resolver problemas con álgebra», se proponen tres problemas que pueden ser resueltos mediante el álgebra en mayor o menor grado, acompañando a los estudiantes en su resolución a partir de preguntas guiadas que dan pie a diferentes reflexiones:

• Cómo el álgebra facilita la resolución de un problema aritmético en el que los datos son numéricos y la solución que se busca también es un número, el problema conduce a la construcción de una expresión algebraica donde será necesario controlar la magnitud que representa cada variable y las unidades en las que se expresan los valores.

Cada problema se plantea de manera abierta al principio (izquierda) para desgranarlo posteriormente, ofreciendo oportunidades para la reflexión del estudiante.

• El segundo problema sirve para poner sobre la mesa dos cuestiones importantes: que una letra no representa un objeto, sino una cantidad de magnitud asociada, y que una expresión algebraica ha de ser coherente en términos de unidades.
• En el último de los problemas, al contrario que en los dos anteriores, un abordaje mediante razonamientos de corte algebraico (y las manipulaciones sintácticas consiguientes) resulta más enrevesado que un razonamiento aritmético. Es decir, el álgebra es una herramienta fabulosa, pero a veces lleva a complicarse más de lo necesario.

Una vez realizado este trabajo de resolución de problemas, la unidad continúa con la resolución de sistemas de ecuaciones. Si bien no es la primera vez que nuestro alumnado utiliza dos variables en sus expresiones algebraicas, pues en la unidad de lenguaje algebraico ya se jugó a comparar y calcular la diferencia de tales expresiones, es ahora cuando estudiamos los sistemas como tales. No obstante, antes de ello, comenzaremos reflexionando sobre la información que podemos extraer de una combinación lineal. La situación inicial consiste en tratar de conocer los precios de una alita y un nugget de pollo a partir del precio de una combinación concreta de estos elementos que aparece en un anuncio. Tras pedir a los estudiantes que expresen la situación con álgebra, preguntamos de forma exploratoria si es posible determinar estos precios de un modo inequívoco, así como si podemos averiguar el precio de otras combinaciones.

El precio de un menú nos permitirá aprender sobre expresiones lineales con dos variables y, en última instancia, sobre sistemas de ecuaciones.

Ahora, con más información, tal vez sí que podamos averiguar el precio de una alita y un nugget, si es que cada alita y cada nugget siempre valen lo mismo (aquí hay alumnado que conecta con la idea de condición de regularidad, de la unidad de proporcionalidad). Así, al expresar esto algebraicamente construimos el primer sistema de ecuaciones, habiendo enlazado el álgebra con el discurso más aritmético (control semántico en el contexto) que permitiría resolver este tipo de problemas. El andamiaje que ofrece la lección fomenta poner en juego diferentes técnicas de resolución, dejando en segundo plano el darles nombre, cosa que recomendamos dejar, en todo caso, para el final (sustitución, igualación, reducción).

¿Quieres saber más sobre las propuestas didácticas de Math Bits?

Si estás interesado en conocer una propuesta pedagógica altamente motivadora para tus estudiantes, basada en la investigación y el descubrimiento guiados, ponte en contacto con nosotros y te daremos acceso a las primeras unidades de muestra.

Referencias

Cid, E. (2015). Obstáculos epistemológicos en la enseñanza de los números negativos. Tesis doctoral. Zaragoza, España: Universidad de Zaragoza.

Cid, E., y Bolea, P. (2010). Diseño de un modelo epistemológico de referencia para introducir los números negativos en un entorno algebraico. En: A. Bronner et al. (Eds.), Diffuser les mathématiques (et les autres savoirs) comme outils de connaissance et d’action (pp. 575-594). Montpellier, Francia: IUFM de l’Académie de Montpellier.

Cid, E., Muñoz-Escolano, J. M., y Ruiz-Munzón, N. (2020). Research on negative numbers in school algebra. En: M. Bosch et al. (Eds.), Working with the Anthropological Theory of the Didactic in Mathematics Education. A Comprehensive Casebook (pp. 61-76). Londres, Reino Unido, y Nueva York, EE. UU.: Routledge.

Cid, E., y Ruiz-Munzón, N. (2011). Actividades de estudio e investigación para introducir los números negativos en un entorno algebraico. En: M. Bosch et al (Eds.), Un panorama de la TAD (pp. 579-604). Bellaterra (Cerdanyola del Vallès), España: Universitat Autònoma de Barcelona.

De la Fuente, A. (2016). Construcción del lenguaje algebraico en un entorno de resolución de problemas. El rol del conocimiento del profesor. Bellaterra (Cerdanyola del Vallès), España: Universitat Autònoma de Barcelona.

Gairín, J. M., y Sancho, J. (2002). Números y algoritmos. Madrid, España: Síntesis.