
Pero, ¿alguien sabe qué son los enteros? ¿Cómo nos ayuda lo aprendido para construir los enteros en la resolución de ecuaciones?
Terminamos de construir los números enteros en esta lección. Ahora sí, el alumnado será plenamente consciente de que trabaja con este nuevo objeto matemático. Estos «números con signo» permiten modelizar con una sola expresión algebraica situaciones para las que, de lo contrario, serían necesarias varias expresiones.
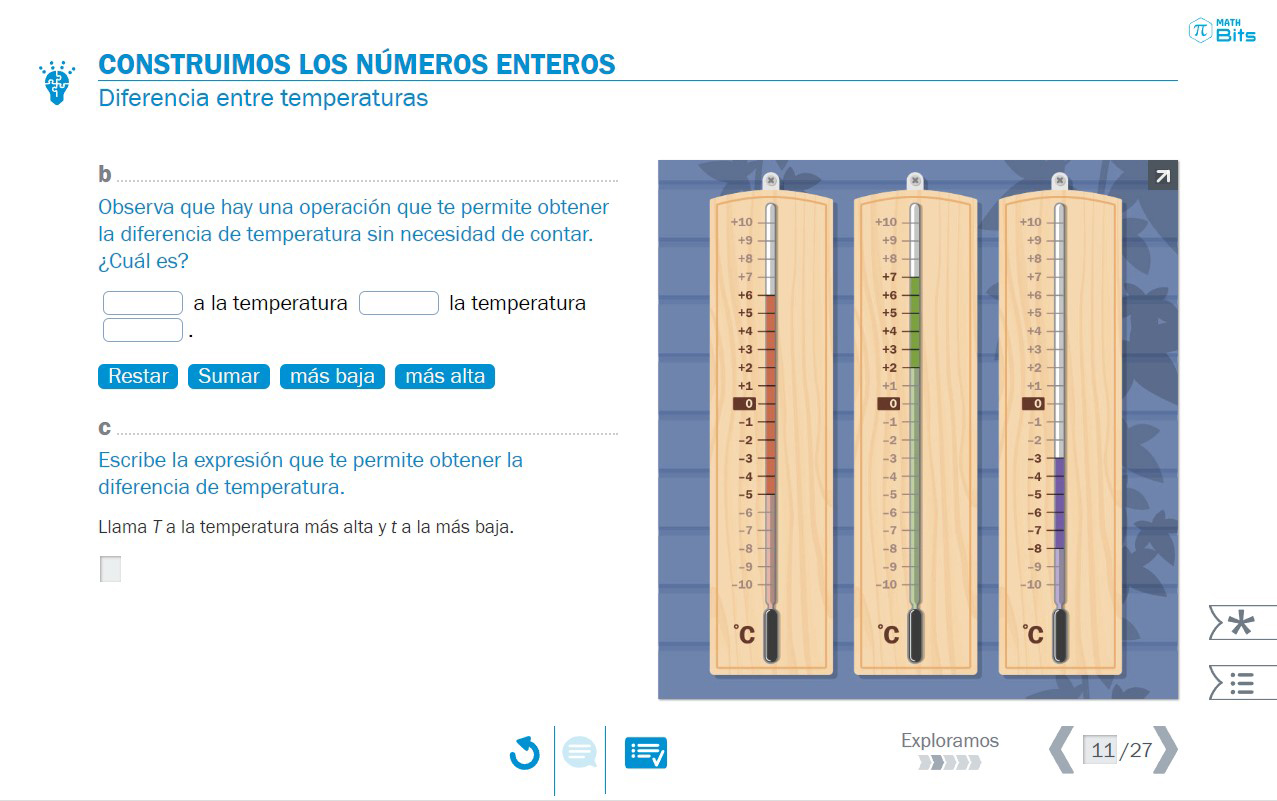
- Construcción de una fórmula (expresión algebraica) que modeliza la diferencia de temperaturas. Sin los enteros, ¿nos bastaría con una sola fórmula?
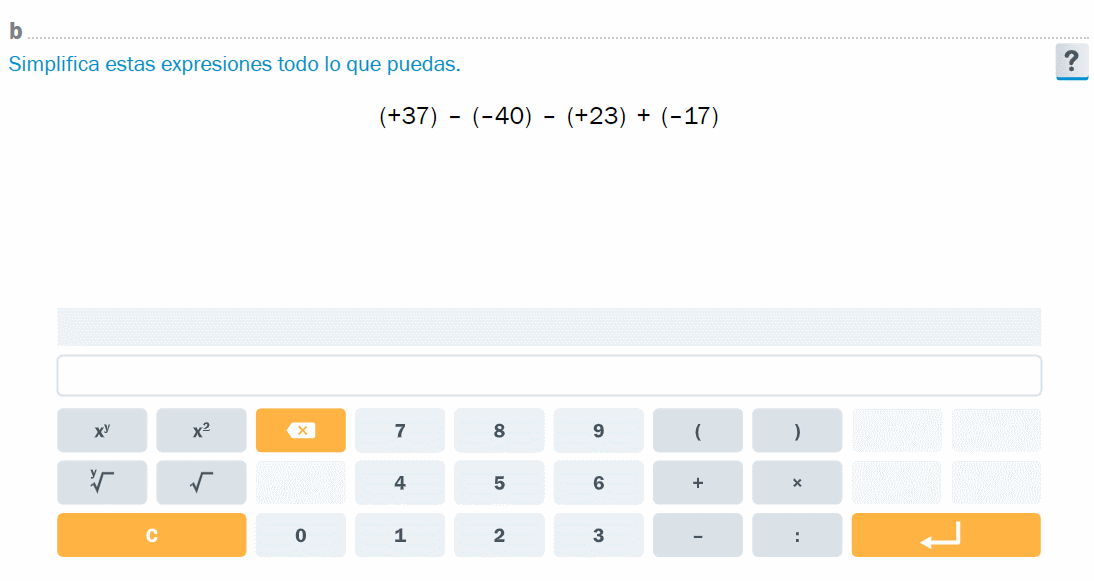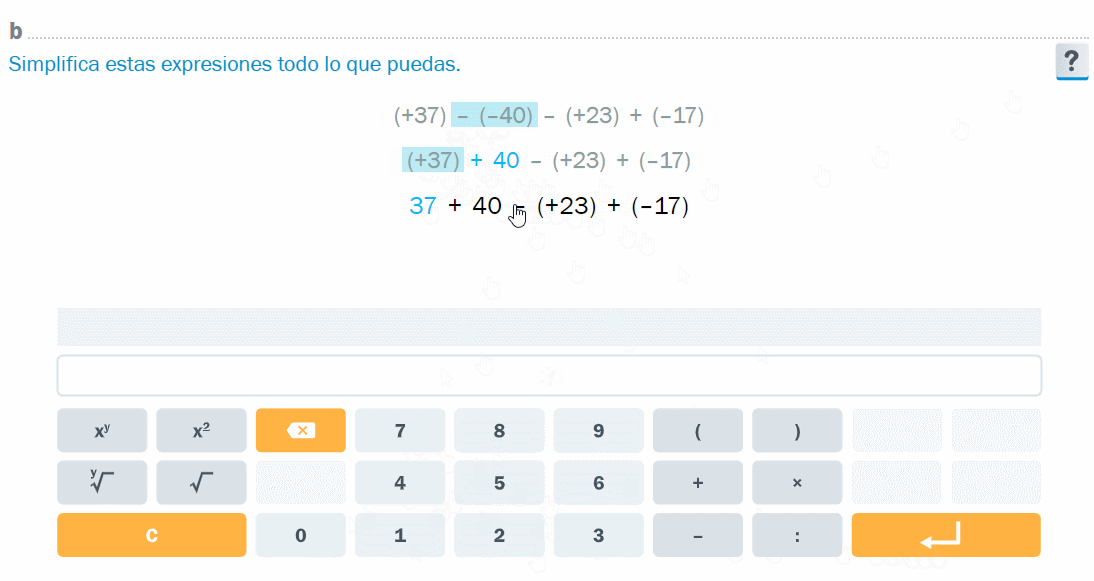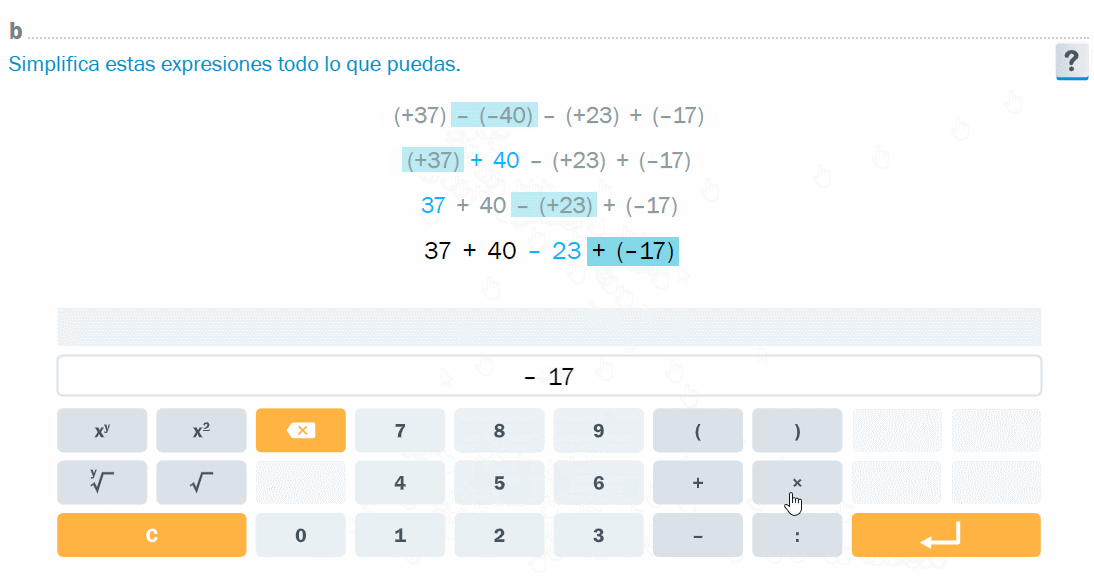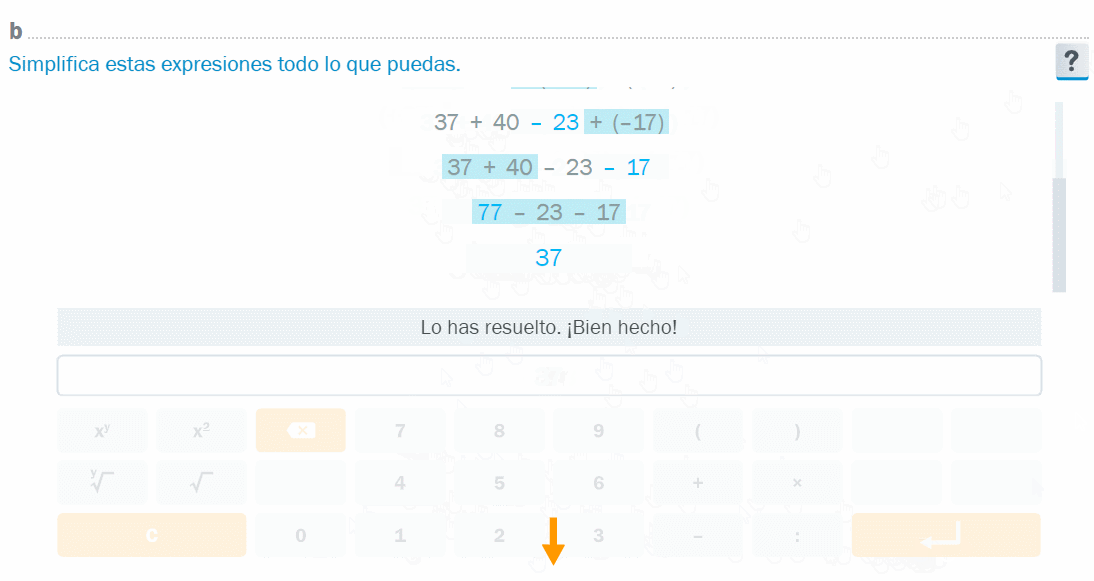
- El manipulador de expresiones permite desarrollar modos de hacer algebraicos. En la animación, simplificación de una expresión con números enteros en notación completa (entre paréntesis y con su signo)
Seguiremos utilizando el entorno algebraico para explorar de manera justificada las operaciones con los enteros y sus propiedades, que son diferentes a las de los números naturales. En cuanto al orden de los enteros, por ejemplo, ¿por qué -8 es menor que -2? No hemos de conformarnos con dar el argumento de que -8 ºC es una temperatura menor que -2 ºC, porque también podría decirse, coloquialmente, que «hace más frío». Será el estudio de lo que ocurre con la diferencia lo que permita dar argumentos sólidos. Una vez hecho todo esto pasaremos a visitar la usual representación de los enteros en la recta numérica.
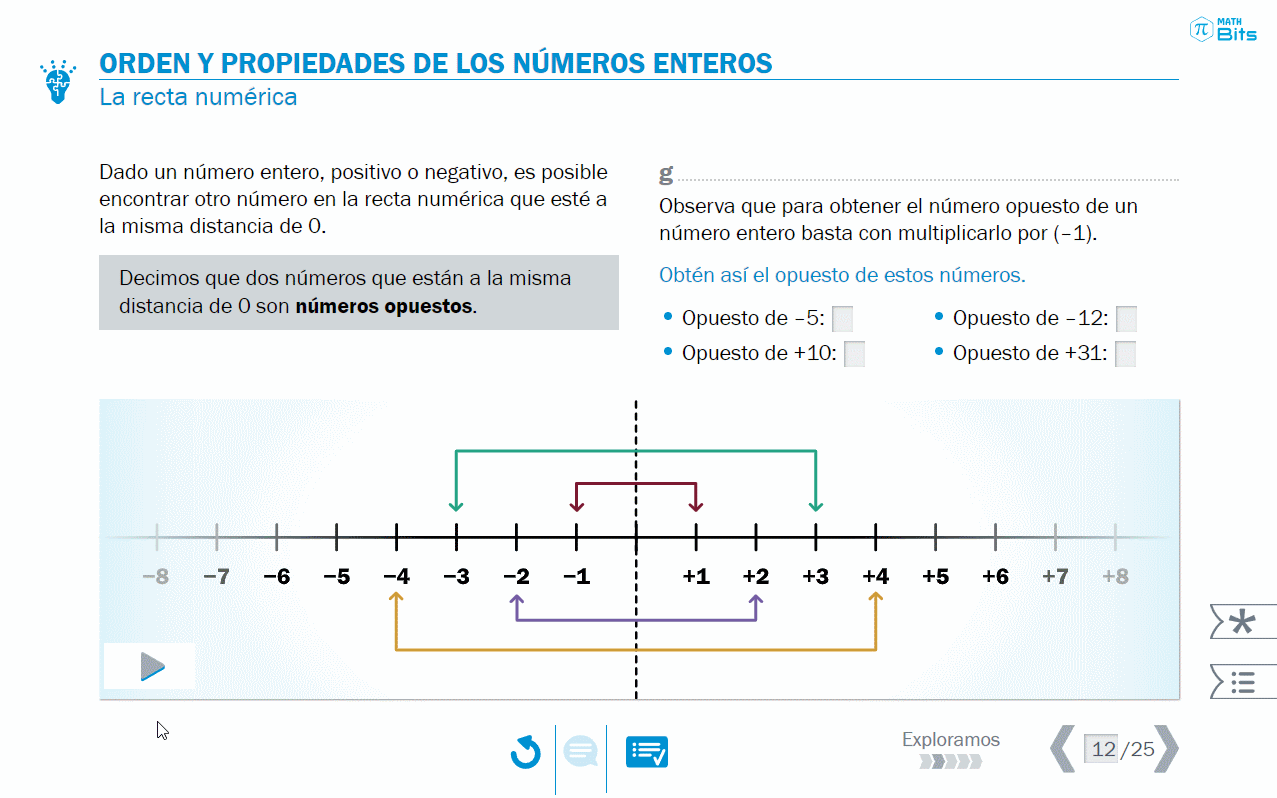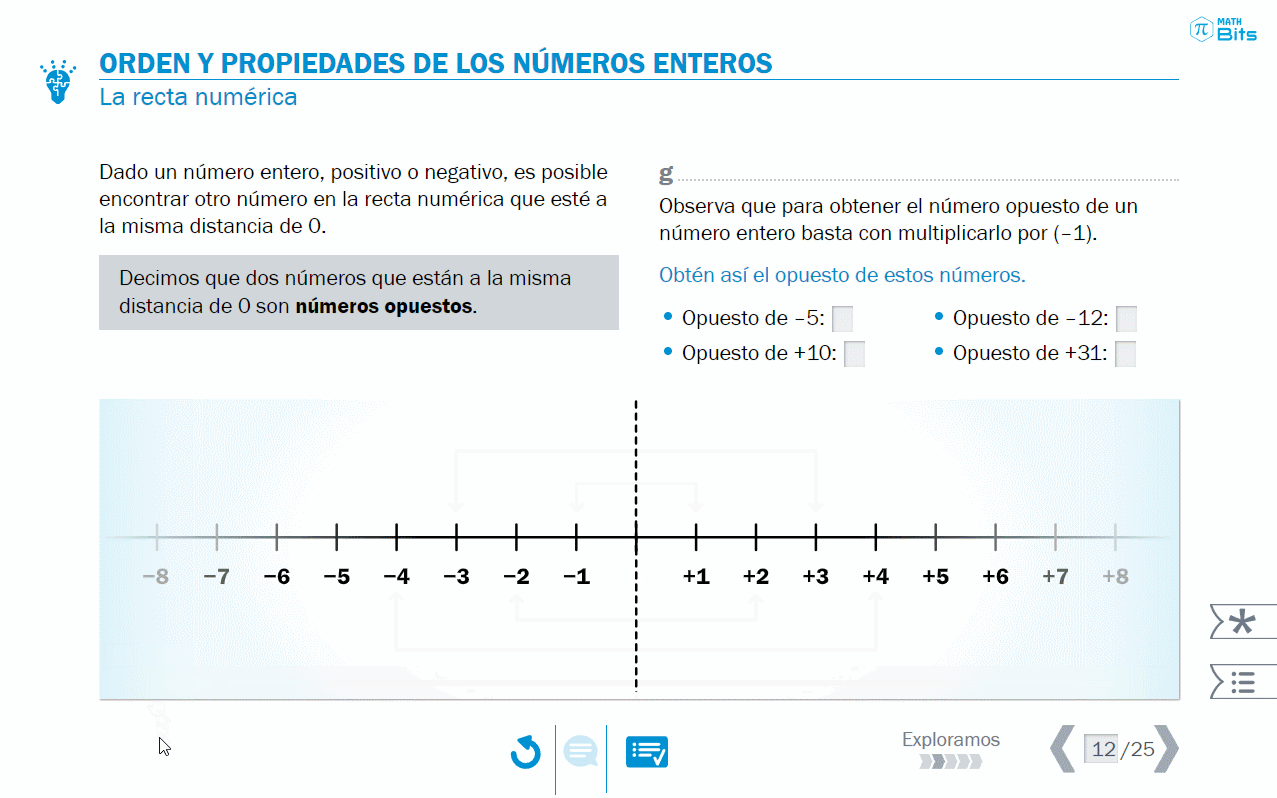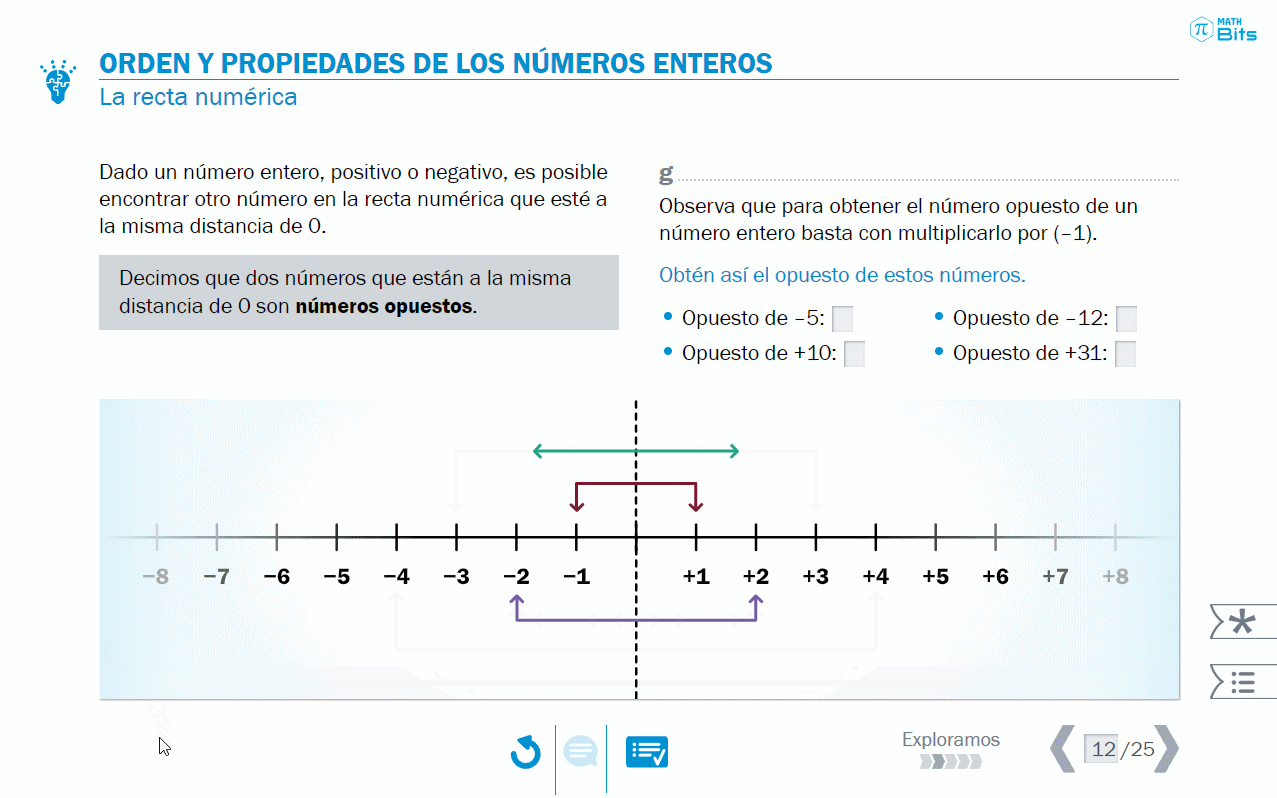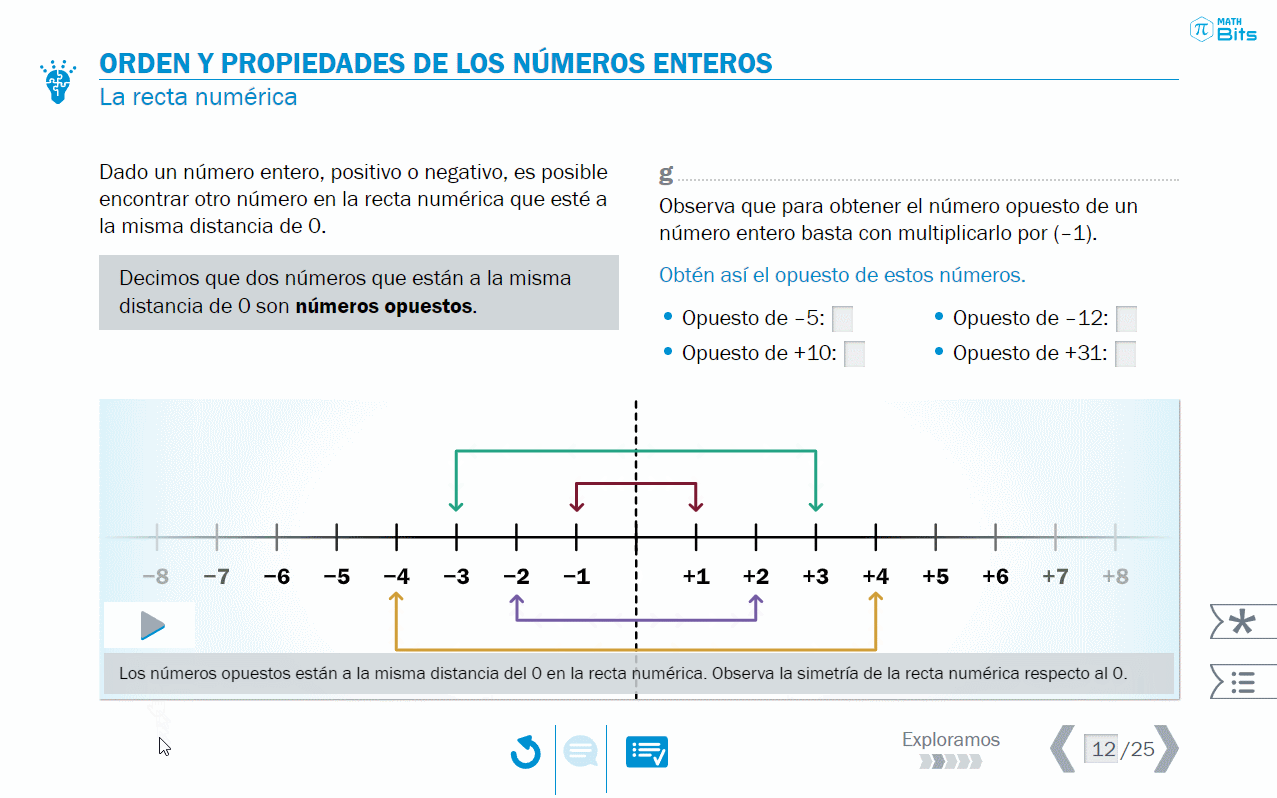
- Reflexión sobre las propiedades de los números enteros sobre la recta numérica. Por ejemplo, en los naturales no existía el concepto de número opuesto.
Si bien en la unidad ‘Lenguaje Algebraico’ aparecen situaciones donde se plantean igualdades y desigualdades algebraicas a partir de las cuales hay que averiguar valores concretos de las variables, ahora abordaremos las ecuaciones explotando la idea de diferencia entre expresiones algebraicas. Esto nos permitirá resolver los más variados problemas y conectar con lo visto anteriormente. Además, el potencial de la idea de diferencia en la resolución de ecuaciones es enorme. No en vano, más adelante, las ecuaciones tienden a presentarse en la forma canónica, igualando a cero.
- La comparación de expresiones algebraicas nos llevó a estudiar la diferencia. Aquí, una actividad introductoria que conecta con conocimientos previos y razonamientos intuitivos.
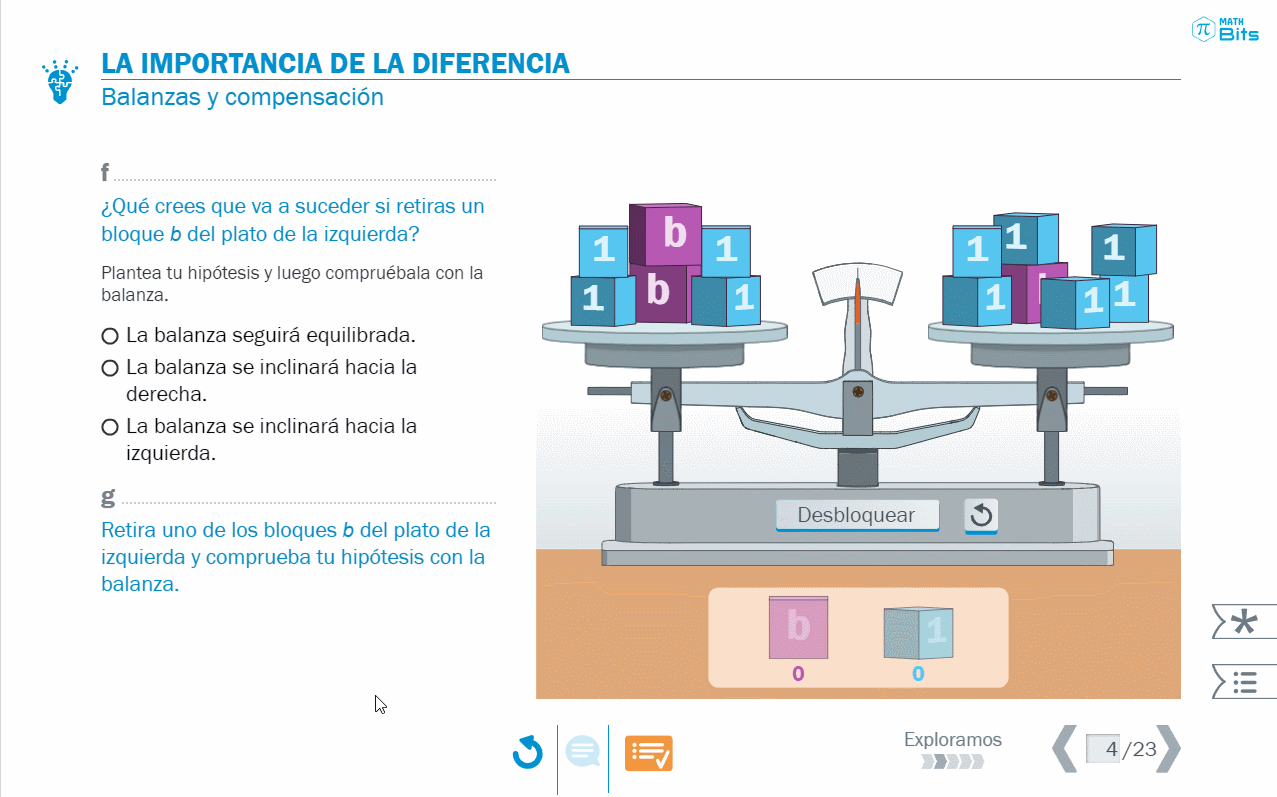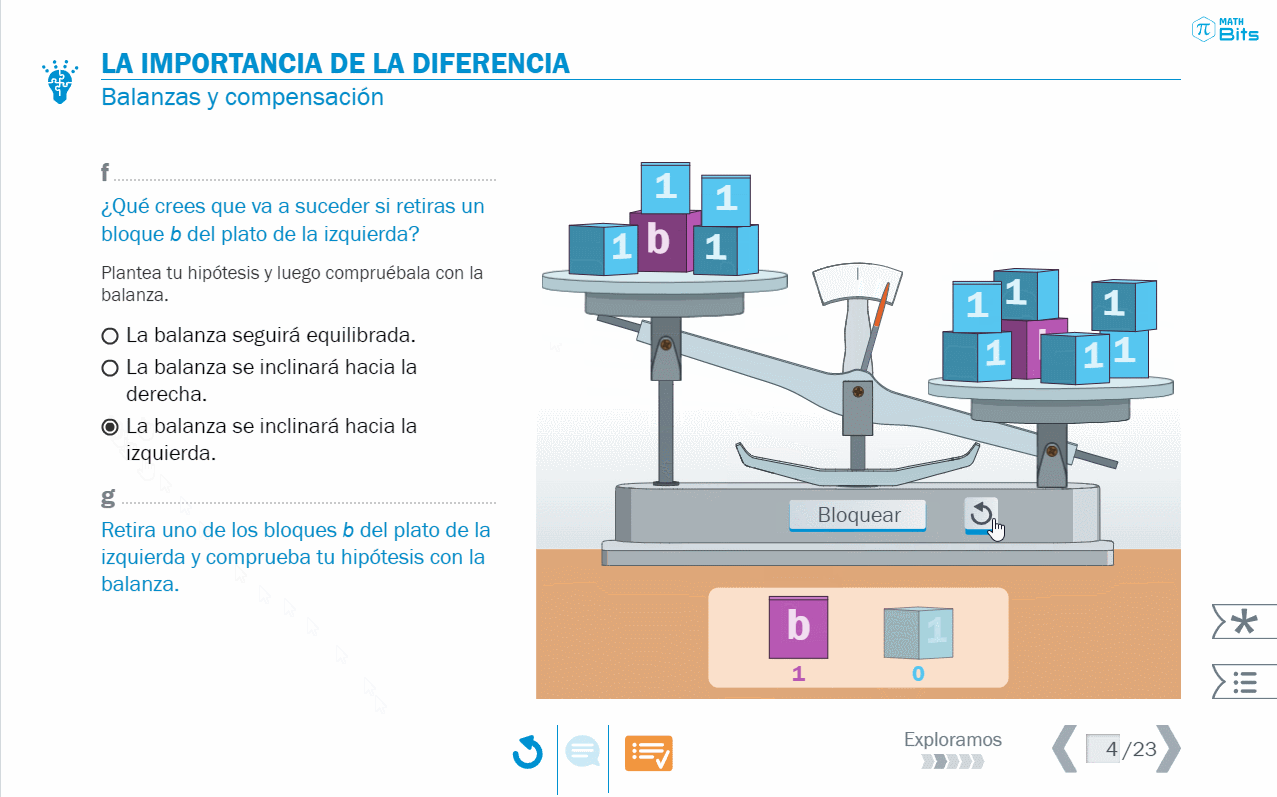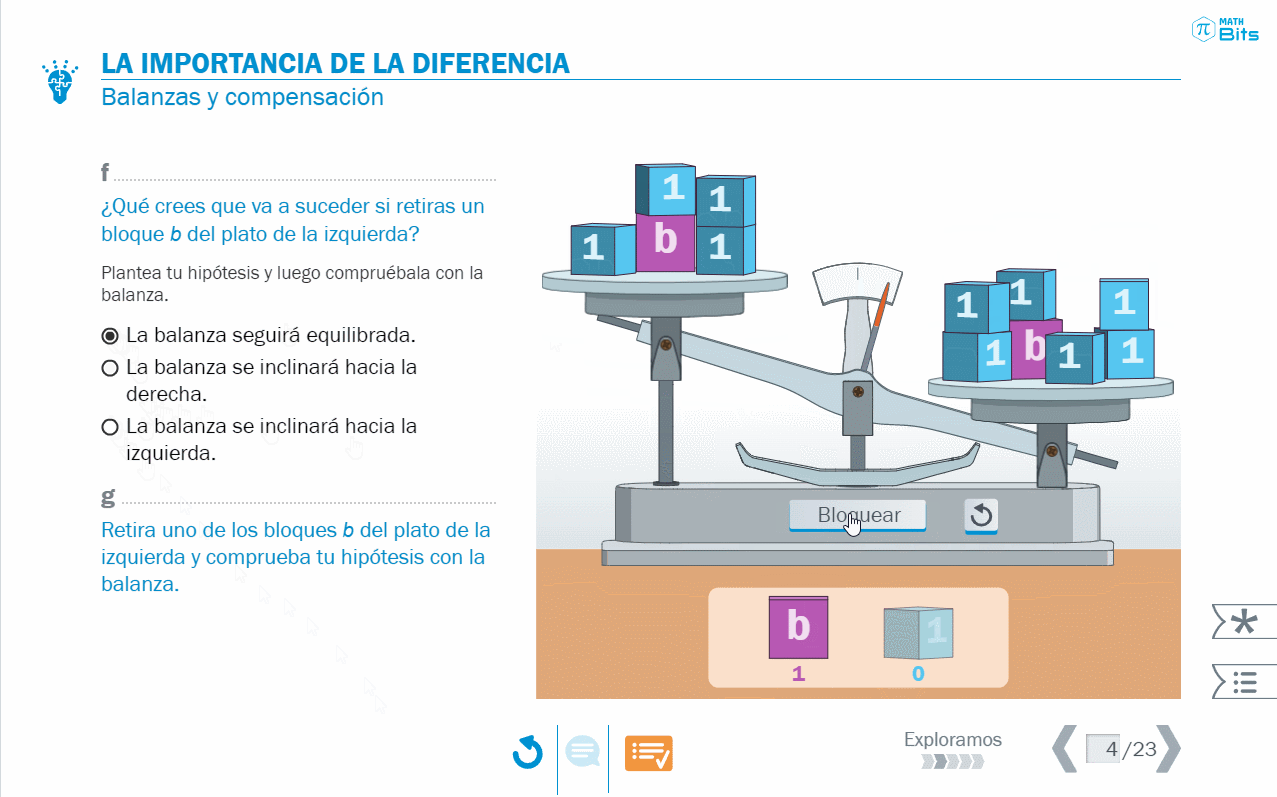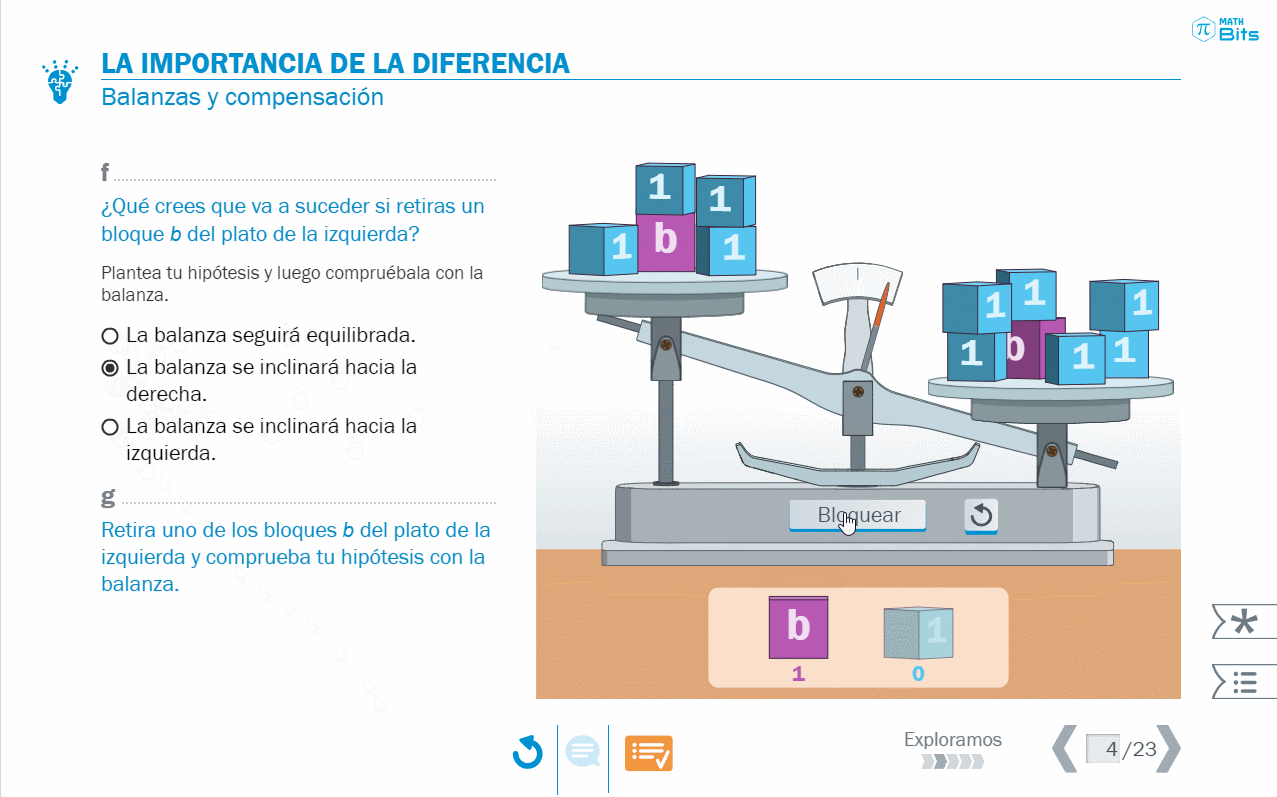
El símil de la balanza da pie a argumentaciones en torno a la noción de compensación y a abordar el concepto de ecuaciones equivalentes desde un punto de vista complementario a la idea de diferencia.
- La resolución de ecuaciones a través del modelo de la balanza nos permite dar sentido, de manera inicial, a lo que ocurre con la diferencia entre los miembros de una ecuación.
Finalmente, con todo lo aprendido a través de las situaciones que se han explorado, se plantean nuevos problemas en los que el álgebra ayuda como instrumento para explicar, precisar razonamientos y llegar a una solución.
- Recurso interactivo ‘El adivinador de números’ (el número que hemos pensado es el 59)
















Deja una respuesta