
El paso de la aritmética al álgebra es un punto de inflexión al que, con demasiada frecuencia, no se le presta toda la atención que merece. Así, no es extraño que al comienzo de la ESO el álgebra se plantee «como la aritmética, pero con letras en lugar de números». Y nada más lejos de la realidad.
En esta transición, se producen cambios significativos que hay que tener en cuenta:
- Cambia el significado de las letras, que hasta ahora se habían podido utilizar para simbolizar unidades de medida.
- Cambia, también, el significado de los signos + y –.
- La resta, se transforma en diferencia.
- Las cuatro operaciones aritméticas quedan reducidas a dos.
- Y, por supuesto, cambia el significado del signo =, que evoluciona hacia una idea de equivalencia.
Esta unidad de Math Bits pretende que el alumnado se familiarice con todos estos cambios. La red de notaciones y símbolos algebraicos no puede aparecer ante sus ojos sin darle significado, pues de lo contrario, reducimos este fascinante aspecto de las matemáticas a la aplicación de reglas vacías.
Al mismo tiempo, el lenguaje algebraico nos da la oportunidad de construir el concepto de número entero (aspecto que culminará en la siguiente unidad). Es sabido que los modelos concretos basados en manipulativos, o en el uso de contextos como termómetros o deudas, plantean obstáculos conceptuales insalvables; en cambio, los números enteros surgen de forma natural por una necesidad puramente matemática en el mundo del álgebra.
Estos son algunos de los recursos destacados que encontraréis en la unidad ‘Lenguaje algebraico’ de Math Bits:
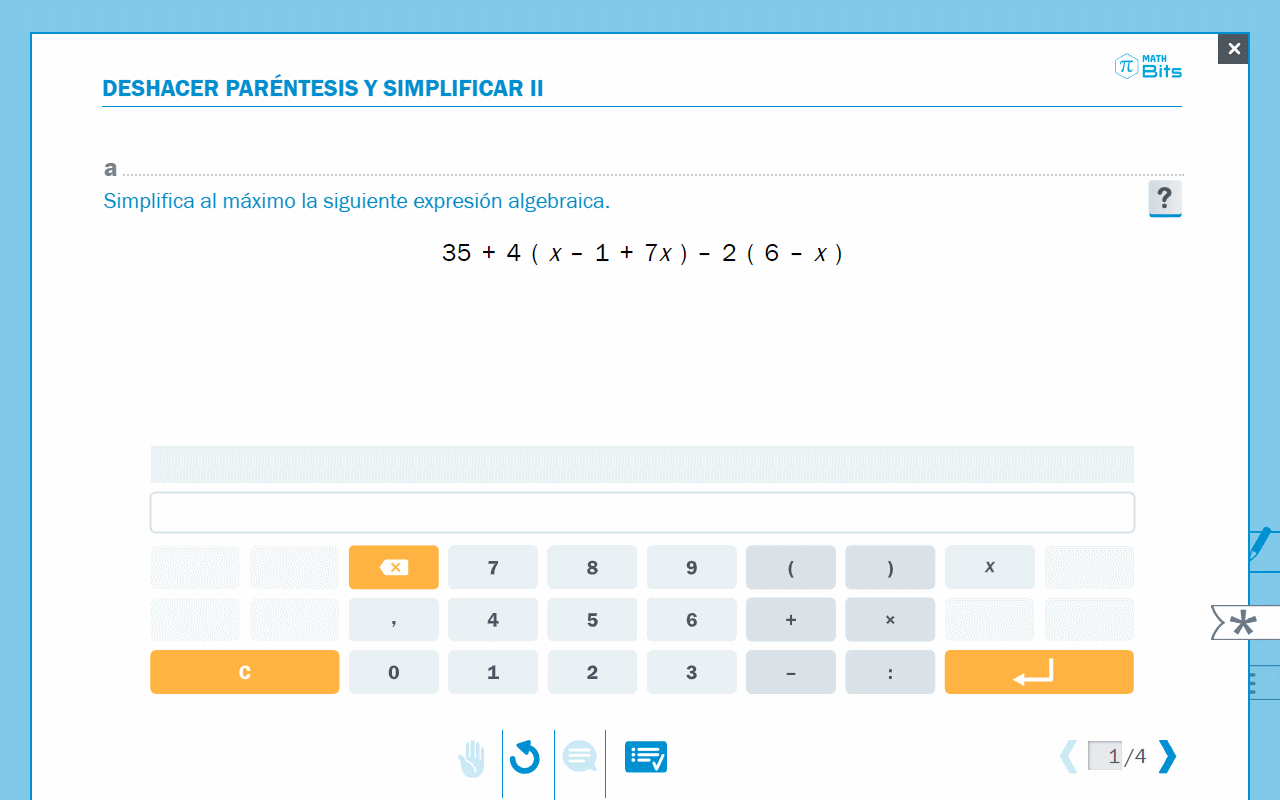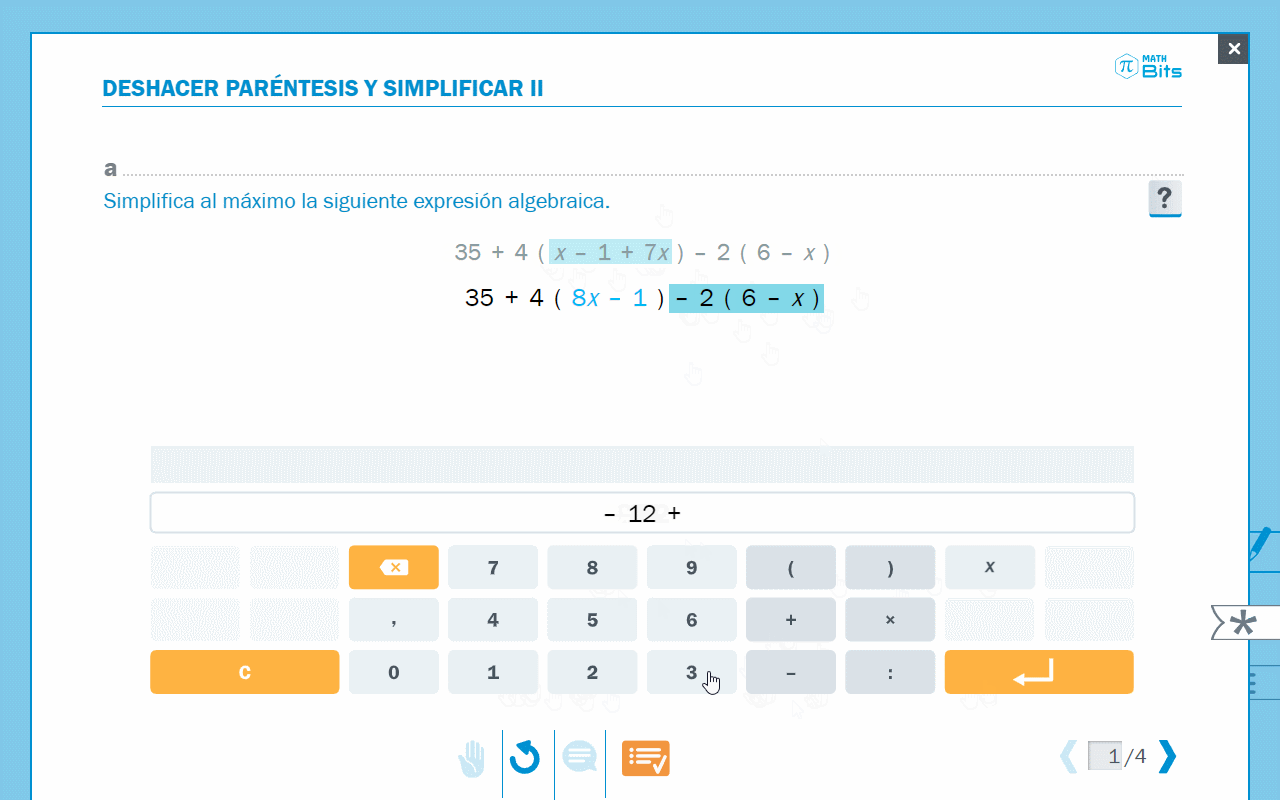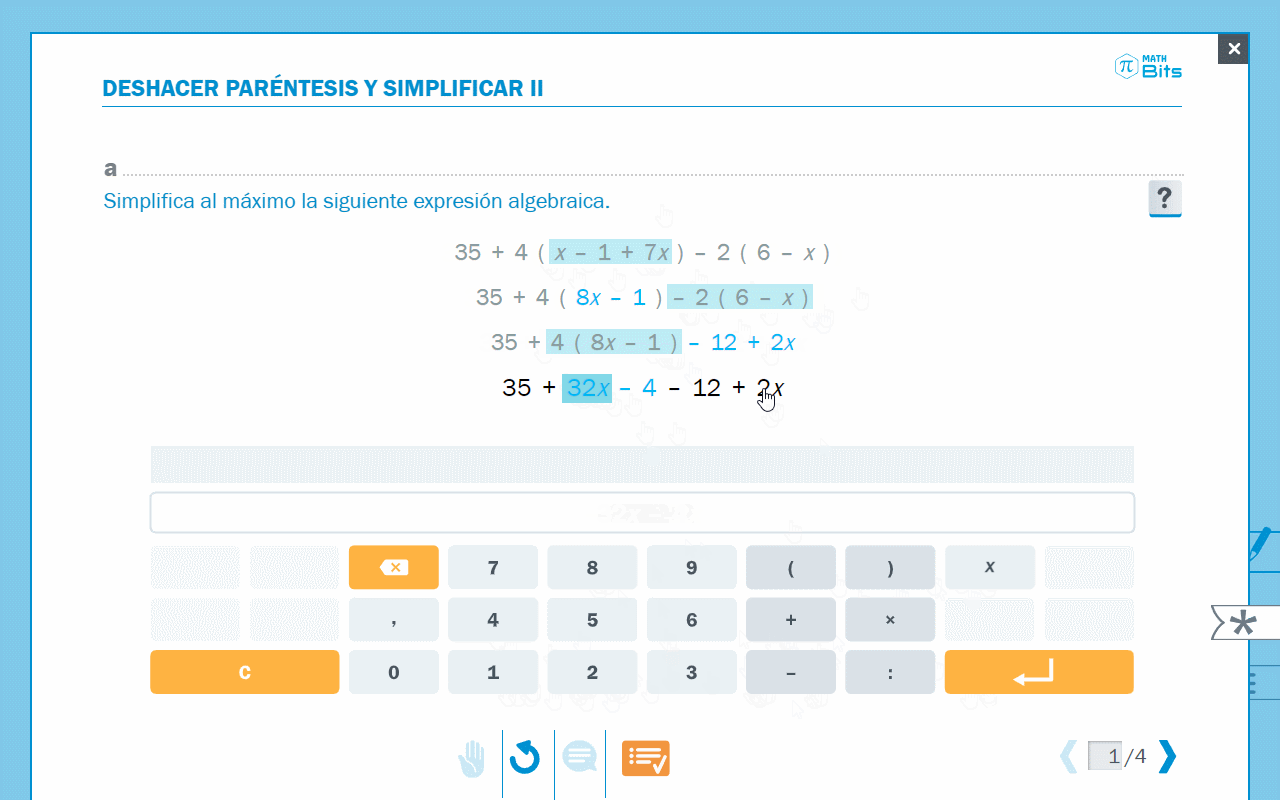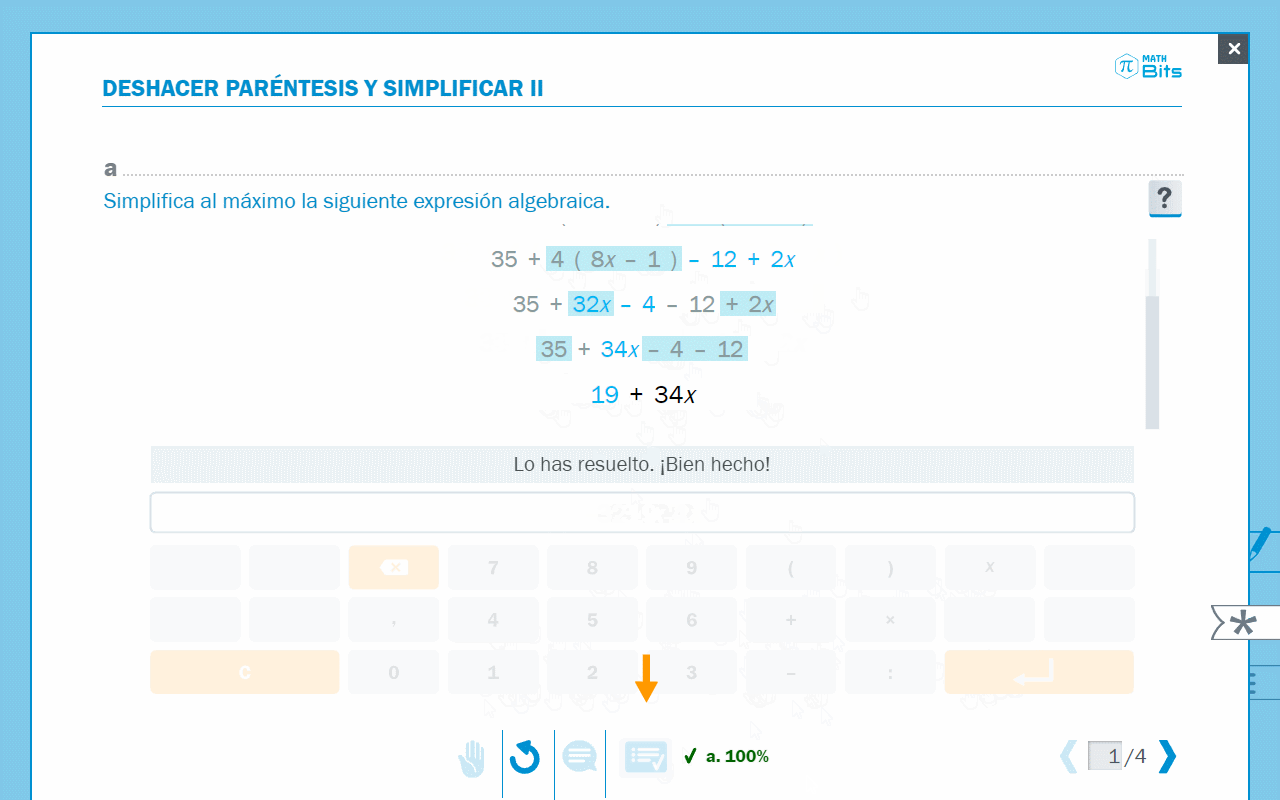
- Editor para simplificar expresiones algebraicas.
- Animaciones para interpretar la comparación de expresiones algebraicas.
- Ejercicio de colocación de paréntesis para expresar diferencias entre expresiones algebraicas.
- Recursos interactivos para comprender que hay igualdades y desigualdades que pueden ser ciertas o falsas en función del valor que se asigne a la variable.
- Juego de adivinación [matemática/basado en álgebra].
Animación donde se observa la simplificación de expresiones algebraicas.

















Deja una respuesta