
Las unidades de Math Bits concluyen con tres lecciones de tipo evaluativo que remarcan la importancia de emplear la evaluación en matemáticas para aprender. Aunque todas las actividades en todas las fases anteriores ya conllevan una evaluación continua, el objeto de terminar la lección con tres actividades explícitamente evaluativas, enfocadas en los mismos objetivos de aprendizaje y con similar dificultad, tiene su razón de ser. Tal propuesta se basa en los principios del mastery learning (método que considera que el proceso de aprendizaje no termina con una prueba de evaluación, sea cual sea su resultado, sino que propone continuar dicho proceso hasta que el resultado sea satisfactorio) y de la «evaluación para el aprendizaje» (o evaluación formativa), que entienden la evaluación como un proceso de aprendizaje en sí mismo.
¿Por qué Math Bits propone realizar tres pruebas al final de cada unidad?
Empecemos por lo más básico: cuando la evaluación es explícita, los estudiantes dan mayor relevancia a la tarea y prestan mayor atención. Ahora bien, el hecho de ofrecer múltiples oportunidades para evaluar su desempeño reduce la ansiedad que algunos alumnos experimentan frente a las pruebas, pues aprecian que el riesgo en cada una se diluye. Esto les permite enfocarse más en la prueba, lo que repercute en su desempeño y en el aprendizaje que obtienen al realizarla. Además, puesto que las tres pruebas abordan los mismos objetivos de aprendizaje, los estudiantes comprenden que tendrán la ocasión de enmendar sus errores en nuevas oportunidades. Esto no solo reduce su ansiedad, sino que hace que su atención al feedback, que podemos proporcionar entre cada prueba, se multiplique.
En efecto, una de las mejores formas de aplicar esta evaluación múltiple consiste en dedicar sesiones intermedias entre cada prueba para proporcionar feedback formativo. Podemos hacerlo de varias maneras:
- Ofreciendo explicaciones a toda la clase sobre aquellas actividades que hayan conllevado mayores dificultades (podemos identificarlas fácilmente a partir de los datos de la corrección automática).
- Activando el feedback que contienen todas las actividades de Math Bits y emplazando a los estudiantes a revisarlo.
- Poniendo en juego estrategias de aprendizaje cooperativo, en que los estudiantes que hayan resuelto bien unas actividades ayuden a los que hayan tenido problemas. Esta práctica resulta especialmente deseable pues se beneficiarán de ella tanto los estudiantes que reciben la ayuda como los que la prestan. En efecto, la investigación en aprendizaje cooperativo muestra que cuando un estudiante enseña a sus compañeros consigue que sus conocimientos devengan más profundos, duraderos y transferibles.
El feedback es uno de los factores que mayor efecto tienen en el aprendizaje, pero para que esto sea así es necesario que el estudiante aprecie su utilidad. Como apuntábamos previamente, esto es lo que conseguimos con múltiples pruebas que evalúan los mismos objetivos de aprendizaje, puesto que con ello el estudiante entiende que el feedback le puede ayudar en la siguiente oportunidad.
Evaluación de matemáticas de forma múltiple
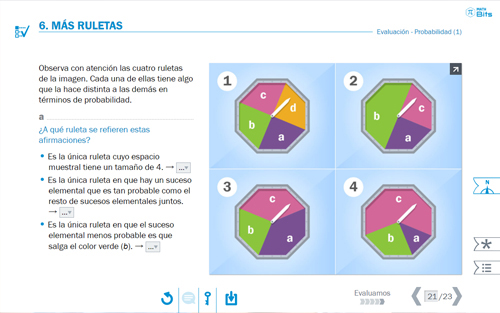
Actividades evaluativas al final de cada lección.
La idea de una evaluación múltiple también contribuye a mejorar las creencias que los estudiantes tienen sobre cómo funciona el aprendizaje y cómo se ven ellos en calidad de estudiantes. Esto es así porque la oportunidad de poner a prueba su desempeño en más de una ocasión les permite apreciar (con hechos y no solo con palabras) que cometer un error no es una evidencia de una supuesta incapacidad para aprender, sino un elemento intrínseco del proceso de aprendizaje, del que pueden aprender para superarse. Por tanto, esta evaluación hace posible que el alumno esté más abierto a aprender de una de las fuentes más importantes de aprendizaje: los errores.
Con todo, esta manera de evaluar no solo contribuye al aprendizaje por los motivos expuestos, sino que también tiene otros beneficios implícitos. En efecto, una de las revelaciones más interesantes de las ciencias cognitivas sobre cómo aprendemos es que evaluarse, per se, es una de las acciones que más nos ayudan a aprender.
Por un lado, la evaluación implica evocar lo aprendido (recuperarlo de nuestra memoria), y la investigación científica constata que esta acción es una de las que más contribuyen a consolidar el aprendizaje y hacerlo así más duradero, transferible, funcional y productivo. En otras palabras, cuando hacemos el esfuerzo de evocar un conocimiento, ya sea factual, conceptual o procedimental, mejoramos la capacidad de evocarlo de nuevo en el futuro, mucho más que si volvemos a consultarlo. Por lo tanto, el hecho de evaluar lo aprendido no solo sirve para comprobar si el aprendizaje se ha producido, sino que en realidad es un acto de aprendizaje en sí mismo (de los más eficaces, ciertamente). Evaluarse es aprender.
Adicionalmente, el hecho de practicar con los mismos objetivos de aprendizaje varias veces pero de manera espaciada en el tiempo también contribuye como pocas cosas a la consolidación del aprendizaje. Es importante remarcar aquí que se trata de oportunidades para practicar que se producirán en sesiones distintas, entre las cuales, además, el alumno tendrá la oportunidad de recibir feedback sobre la prueba anterior.
Pero aún hay más: los beneficios de este tipo de evaluación aumentan si las pruebas promueven la llamada práctica entrelazada. Se trata de organizar las actividades de manera que los estudiantes deban aplicar los diversos aprendizajes realizados de forma combinada, sin pistas superfluas para resolver las cuestiones, como las que ofrece el hecho de saber a qué tema o apartado corresponde la actividad. Esto flexibiliza el aprendizaje y lo hace más sólido y transferible. En realidad, la práctica entrelazada es otra de las estrategias de aprendizaje más eficaces en el ámbito de las matemáticas.
En definitiva, cuando se emplea adecuadamente, la evaluación puede ser una de las herramientas más eficaces para promover el aprendizaje.
ESCRITO POR Héctor Ruiz Martín – ISTF
@hruizmartin
Referencias:
Bjork, E. L., y Bjork, R. A. (2011). Making things hard on yourself, but in a good way: Creating desirable difficulties to enhance learning. En: M. A. Gernsbacher, R. W. Pew, L. M. Hough y J. R. Pomerantz (Eds.), Psychology and the real world: Essays illustrating fundamental contributions to society (pp. 59-68). Nueva York, EE. UU.: Worth Publishers.
Carpenter, S. K. (2014). Spacing and interleaving of study and practice. En: V. A. Benassi, C. E. Overson y C. M. Hakala (Eds.), Applying the science of learning in education: Infusing psychological science into the curriculum (pp. 131-141). Washington D. C., EE. UU.: Society for the Teaching of Psychology.
Hattie, J., y Timperley, H. (2007). The power of feedback. Review of Educational Research, 77(1), 81-112.
Karpicke, J. D., y Roediger, H. L. (2008). The critical importance of retrieval for learning. Science, 319(5865), 966-968.
Sanmartí, N. (2007). Evaluar para aprender. Barcelona, España: Graó.
Slavin, R. E. (2013). Cooperative learning and achievement: Theory and research. En: W. M. Reynolds, G. E. Miller y I. B. Weiner (Eds.), Handbook of psychology: Educational psychology (2.ª edición, vol. 7, pp. 199-212). Hoboken, EE. UU.: John Wiley & Sons Inc.
Wiliam, D. (2011). Embedded formative assessment. Bloomington, EE. UU.: Solution Tree Press.













Deja una respuesta