Qué es la probabilidad y como enseñarla

Resulta chocante que la enseñanza de la probabilidad quede muchas veces en segundo plano, pues si hay un aprendizaje matemático aplicable a la vida cotidiana, ese es el razonamiento probabilístico. Así, las grandes ideas de la probabilidad nos permiten aprender a gestionar situaciones de riesgo e incertidumbre y contribuyen a que seamos capaces de vivir en sociedad como ciudadanos críticos.

A diferencia de otras ramas de la matemática en las que el mundo de lo sensible nos ofrece experiencias para contrastar nuestras concepciones y poder aprender de manera informal, la probabilidad requiere siempre del análisis sistemático de dichas experiencias. Consideremos, por ejemplo, el clásico juguete para bebés que consiste en una casita con ventanas de formas variadas. Si el bebé toma la forma redondeada para introducirla por la ventana rectangular, el mismo juguete le «dice» que no, que pruebe con otra, debido a que esa pieza nunca podrá pasar por ese hueco. Sin embargo, podemos estar toda la tarde jugando al parchís y afirmar que es menos probable obtener un cinco al lanzar el dado, al pensar que nos costaba mucho conseguir sacar ficha.

Carecer de estas experiencias y no haber tenido la ocasión de reflexionar sobre ellas fomenta la aparición de sesgos de razonamiento. Si no se remedia esta situación, estos sesgos tienden a persistir. El comienzo de la educación secundaria ofrece una oportunidad excelente para subsanar este posible déficit, al mismo tiempo que se sientan las bases para la formalización de los conceptos clave.

Pero ¿qué es la probabilidad?

La respuesta a esta pregunta no es sencilla y está llena de matices. Autoras como Batanero (2005) sintetizan los significados de la probabilidad en educación secundaria atendiendo a las definiciones, lenguajes, situaciones-problema, proposiciones, procedimientos y argumentos que caracterizan a cada uno de ellos:

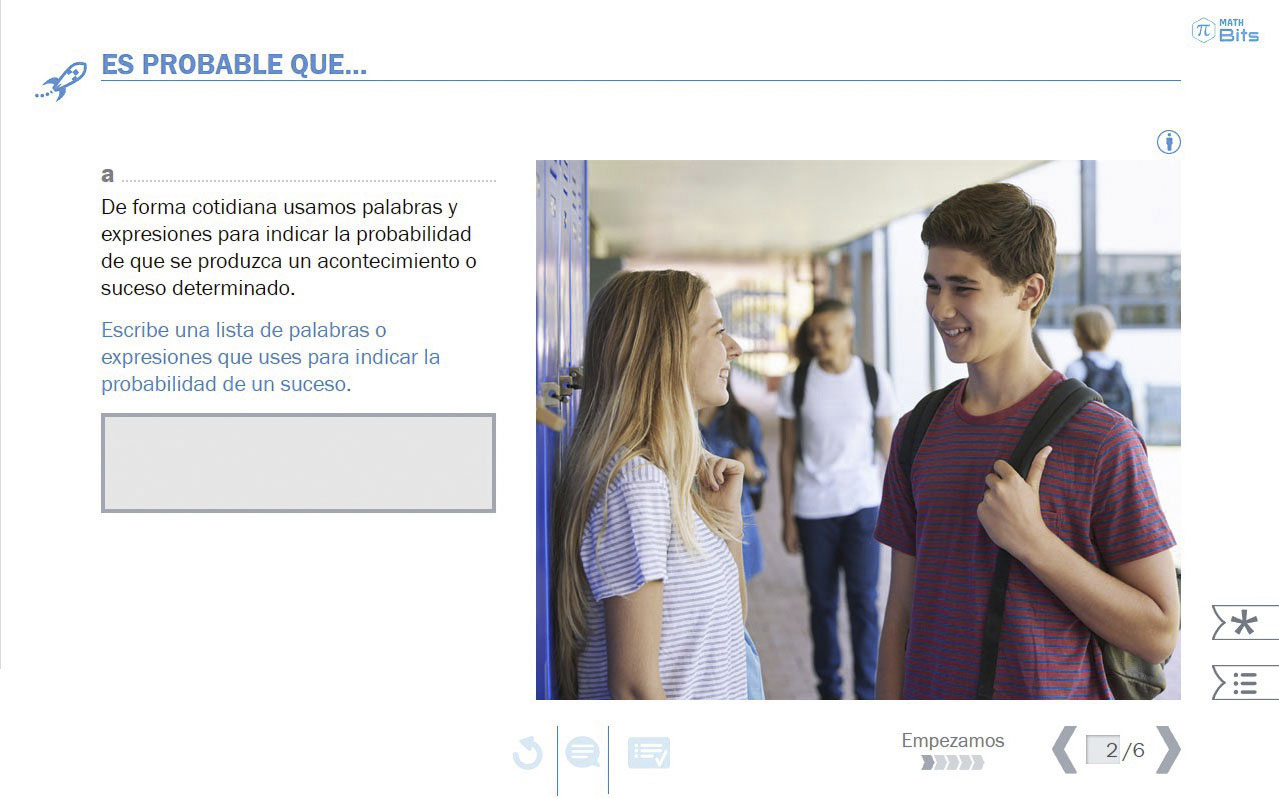
• Significado intuitivo. La probabilidad, como noción matemática, empieza a desarrollarse en el siglo xvii. Ahora bien, sus ideas más intuitivas han acompañado a la humanidad desde tiempos pretéritos, y podemos encontrar juegos de azar en casi todas las grandes civilizaciones de la antigüedad. Estas ideas aparecen también espontáneamente en niños y personas sin formación específica y suelen manifestarse a través de las expresiones que incorpora el lenguaje natural para indicar nuestro grado de creencia acerca de la ocurrencia o no de un suceso.
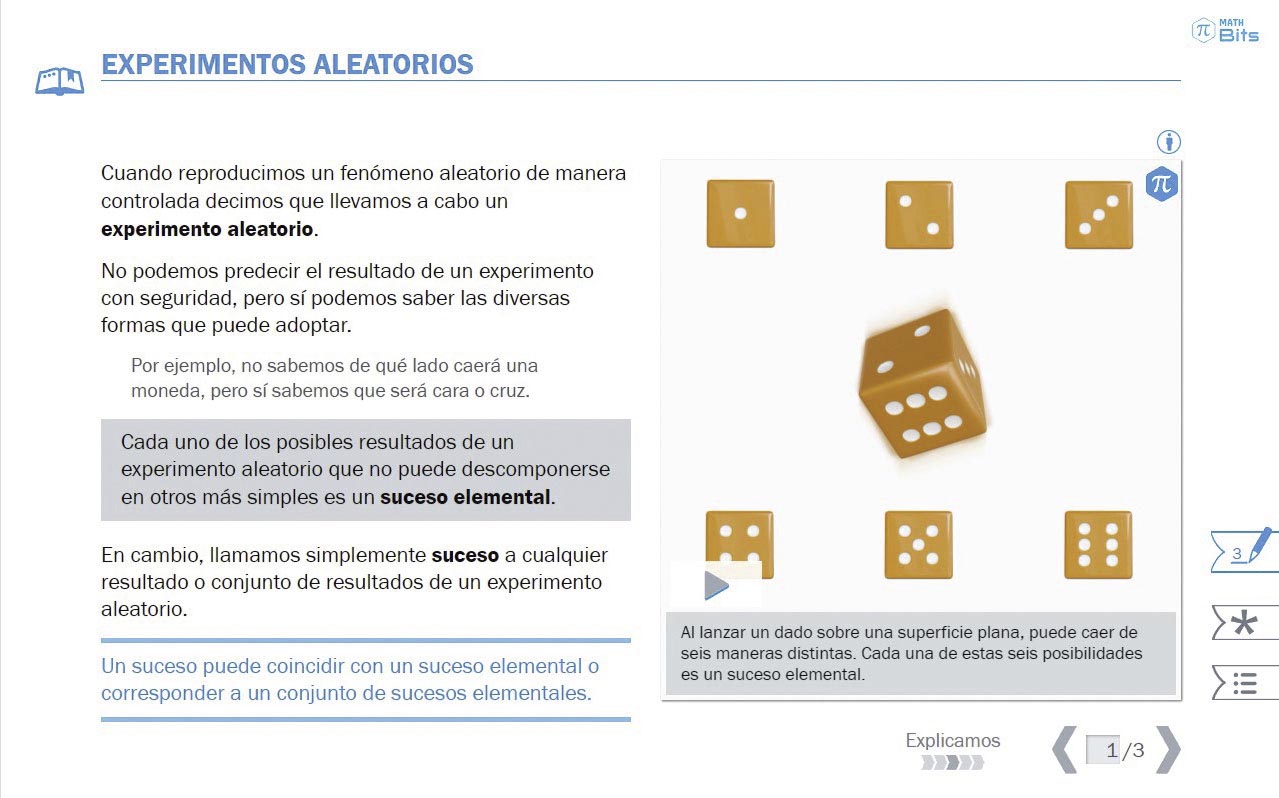
• Significado clásico o laplaciano. Se corresponde con las primeras aproximaciones desde la matemática, a partir de la correspondencia entre Pascal y Fermat. Se sintetiza en la regla de Laplace, en la que se calcula la probabilidad de un suceso como el cociente entre el número de casos favorables y el número total de casos. Esta visión acarrea la necesidad de reducir los fenómenos a un cierto número de casos equiprobables. No es aplicable, por tanto, a situaciones donde no pueda asumirse que los sucesos elementales son equiprobables (lanzamiento de chinchetas, por ejemplo). Este significado emerge de situaciones relacionadas con el cálculo de esperanzas o riesgos en juegos de azar e involucra procedimientos y razonamientos de combinatoria y de proporcionalidad.
• Significado frecuencial. Tiene su origen en la primera ley de los grandes números de Bernoulli. En su momento, esta ley fue aceptada más bien como una simple comprobación empírica de la probabilidad de un suceso calculada previamente de forma teórica. Así, las frecuencias relativas tienden a estabilizarse en torno a valores concretos. Históricamente, fue la formalización del análisis cuando se dispuso de las herramientas teóricas que conectan con rigor la frecuencia relativa con la probabilidad. La conexión con el razonamiento proporcional es evidente, al igual que en el clásico, pero desde un punto de vista diferente.
• Significado subjetivo. El teorema de Bayes formaliza la idea fundamental de este significado: que la probabilidad a priori de un suceso puede revisarse si se dispone de nueva información. Esto implica la pérdida del carácter objetivo de la probabilidad, debido a que la probabilidad de un suceso siempre va a depender de nuestro conocimiento del fenómeno en cuestión.
• Significado axiomático. Los trabajos sobre medida de Borel hicieron posible que, posteriormente, Kolmogorov desarrollara la formalización de la teoría de la probabilidad, independiente del significado subyacente. A partir de entonces, la probabilidad pasó a ser un modelo matemático con multitud de aplicaciones.

Una secuencia didáctica adecuada considerará todos estos significados. Obviamente, el aparataje matemático del significado axiomático solo será posible en bachillerato y en la universidad. El resto de los significados deberían irse desarrollando de forma articulada graduando los planos de abstracción y la complejidad de las técnicas asociadas. A veces, se considera que el significado subjetivo únicamente tiene que ver con los formalismos asociados a la probabilidad condicional y al teorema de Bayes, pero es un significado que debe trabajarse antes de manera informal, a través de situaciones en donde haya que explicitar cómo cambia nuestro grado de creencia acerca de la ocurrencia del suceso en cuestión cuando se dispone de nueva información en el sistema.

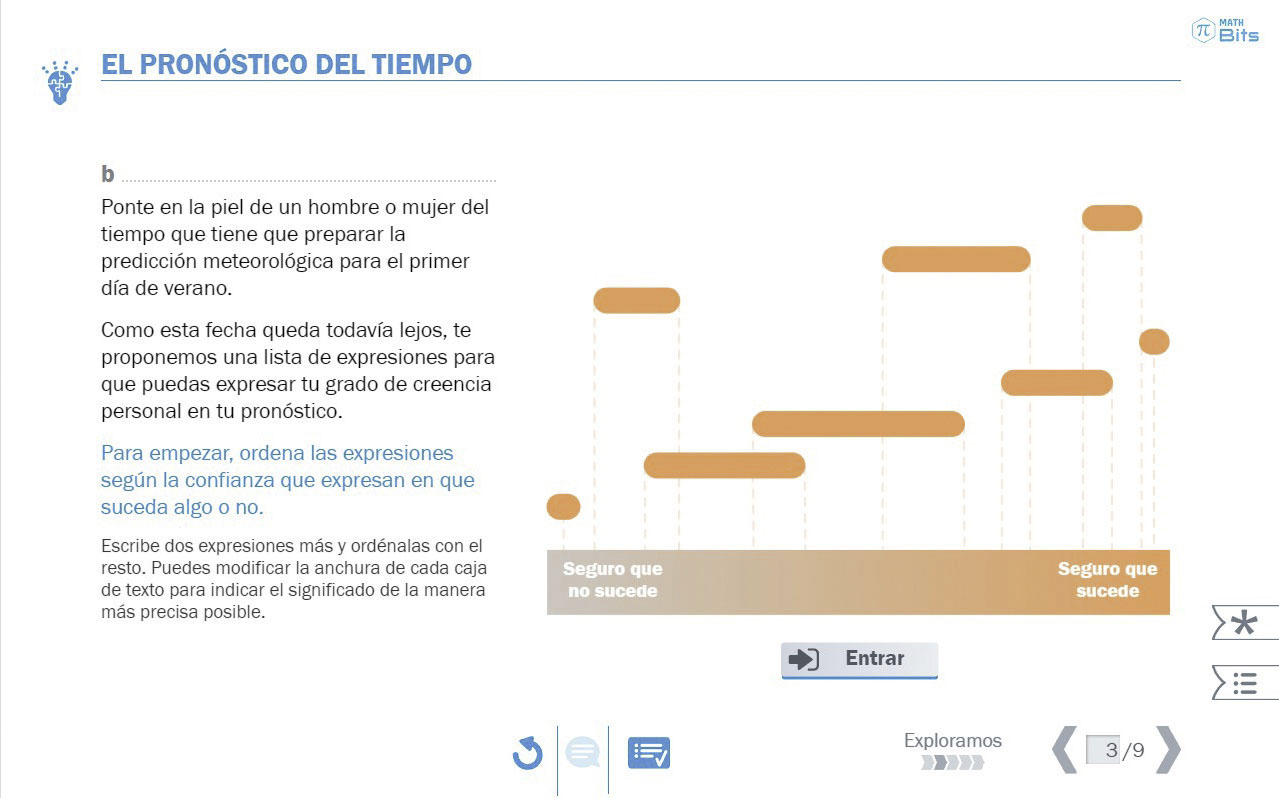
Al tratar de ordenar términos y expresiones del lenguaje cotidiano, surge la necesidad, o posibilidad, de asignar un número a nuestro grado de creencia personal. Es ahí donde se conecta con la escala de la probabilidad, tanto desde el significado clásico como desde el frecuencial. La articulación de estos dos últimos significados requiere una cuidadosa planificación. No se ha de mostrar el significado frecuencial como una simple comprobación empírica del clásico. Por un lado, vamos a tener situaciones que involucren sucesos cuya probabilidad no pueda calcularse teóricamente de manera precisa. Por otro lado, incluso para poder calcular de forma teórica la probabilidad en situaciones que involucran el lanzamiento de dados, extracción de bolas, etc., estamos asumiendo implícitamente un modelo que solo funciona de manera perfecta bajo ciertas condiciones. Por tanto, antes de usar la regla de Laplace, es necesario explicitar la suposición de que los sucesos son equiprobables. Para mostrar esta necesidad será necesario incluir en nuestra secuencia situaciones en donde esta suposición no tenga sentido o conduzca a un error manifiesto.

Didáctica de la probabilidad

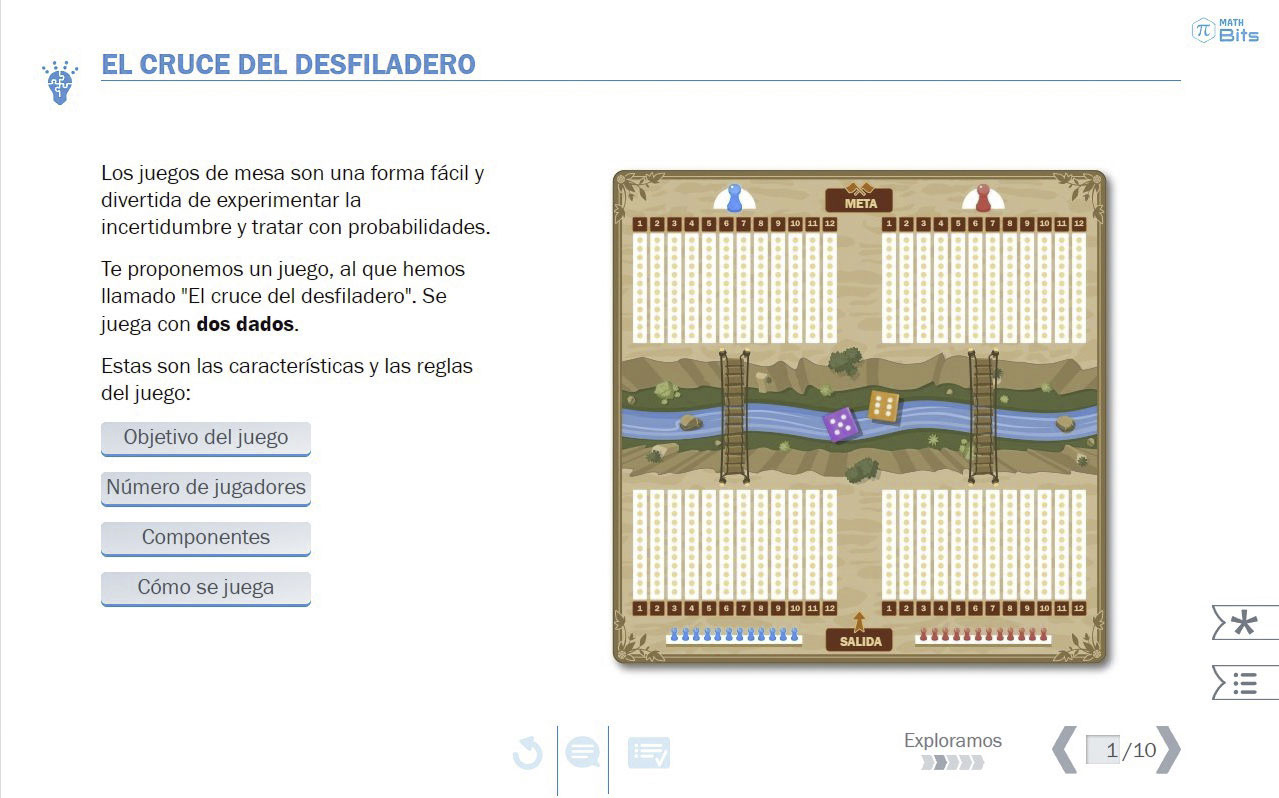
Además de los diferentes significados de la probabilidad, el diseño de la secuencia didáctica tendría que atender a los posibles sesgos de razonamiento. Uno de ellos es el sesgo de equiprobabilidad, que consiste en la creencia en la equiprobabilidad de todos los sucesos asociados a cualquier experimento aleatorio. Esto se identifica, por ejemplo, en una aplicación indiscriminada de la regla de Laplace, sin plantearse si es posible aplicar el principio de indiferencia o si existe algún tipo de simetría. Proporcionar una amplia variedad de situaciones que articulen convenientemente el significado clásico con el frecuencial será indispensable para tratar de eliminar este sesgo o evitar su desarrollo y afianzamiento. 

Otros sesgos de razonamiento son aquellos que surgen al no tener en cuenta el tamaño de la muestra, ni la variabilidad del muestreo o de las repeticiones de un experimento aleatorio. Todo esto entra dentro de lo que se conoce como heurística de la representatividad. Un ejemplo es el conocido como la falacia del jugador, donde ante una racha de resultados, se espera que aumente la probabilidad del suceso contrario en la siguiente repetición del experimento. Por último, el enfoque en el resultado aislado tiene lugar cuando se piensa que cada una de las repeticiones de un experimento aleatorio no guarda relación con las anteriores o posteriores. Está relacionado con dificultades para comprender el significado frecuencial. 

¿Cómo enseñar probabilidad matemática?

La secuencia que se plantea en Math Bits atiende a las consideraciones anteriores y se ubica en un enfoque de enseñanza a través de la resolución de problemas. Así, los alumnos construyen el conocimiento enfrentándose a la resolución de situaciones y problemas diseñados con la intención de hacer emerger los contenidos matemáticos deseados. Al mismo tiempo, este enfoque facilita la conexión con los conocimientos previos del alumnado.

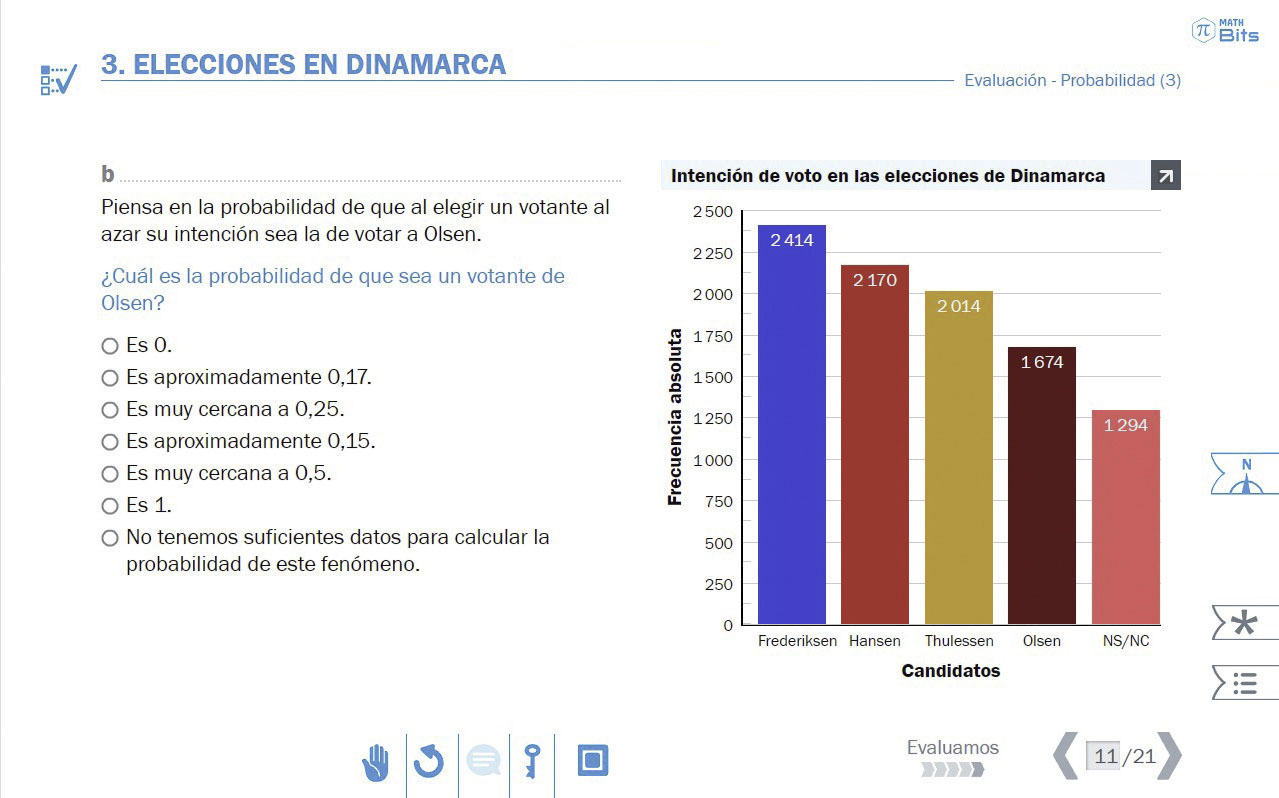
Estos son algunos de los recursos que proponemos para trabajar el enfoque didáctico de probabilidad en Math Bits:

ESCRITO POR
Pablo Beltrán-Pellicer – Universidad de Zaragoza
@pbeltranp
Profesor titular en el área de Didáctica de las Matemáticas en la Facultad de Educación de la Universidad de Zaragoza.

Referencias:

• Batanero, C. (2005). Significados de la probabilidad en educación secundaria. Revista latinoamericana de investigación en matemática educativa, 8(3), 247-264.

• Beltrán-Pellicer, P. y Giacomone, B. (2021). Una propuesta didáctica de probabilidad para el comienzo de la secundaria. Educação Matemática Pesquisa, 23(4), 246-272.

• Konold, C. (1989). Informal conceptions of probability. Cognition and Instruction, 6(1), 59-98. 

• Lecoutre, M. P. (1992). Cognitive models and problem spaces in “purely random” situations. Educational Studies in Mathematics, 23(6), 557-568.

• Tversky, A. y Kahneman, D. (1974). Judgement under uncertainty: Heuristics and biases. Science, 185(4157), 1124-1131.