
El pas de l’aritmètica a l’àlgebra és un punt d’inflexió al qual, amb massa freqüència, no es para tota l’atenció que es mereix. Així, no és estrany que al començament de l’ESO l’àlgebra es plantegi «com l’aritmètica, però amb lletres en lloc de nombres». I res més lluny de la realitat.
En aquesta transició, es produeixen canvis significatius que cal tenir en compte:
- Canvia el significat de les lletres, que fins ara s’havien pogut fer servir per simbolitzar unitats de mesura.
- Canvia, també, el significat dels signes + i –.
- La resta es transforma en diferència.
- Les quatre operacions aritmètiques queden reduïdes a dues.
- I, per descomptat, canvia el significat del signe =, que evoluciona cap a una idea d’equivalència.
Aquesta unitat de Math Bits pretén que l’alumnat es familiaritzi amb tots aquests canvis. La xarxa de notacions i símbols algebraics no pot aparèixer davant dels seus ulls sense que hi donem significat perquè, en cas contrari, reduïm aquest fascinant aspecte de les matemàtiques a l’aplicació de regles buides.
Alhora, el llenguatge algebraic ens dona l’oportunitat de construir el concepte de nombre enter (aspecte que culminarà a la unitat següent). És sabut que els models concrets basats en manipulatius, o en l’ús de contextos amb termòmetres o deutes, per exemple, plantegen obstacles conceptuals insalvables; en canvi, els nombres enters sorgeixen de forma natural per una necessitat purament matemàtica en el món de l’àlgebra.
Aquests són alguns dels recursos destacats que trobareu a la unitat ‘Llenguatge algebraic’ de Math Bits:
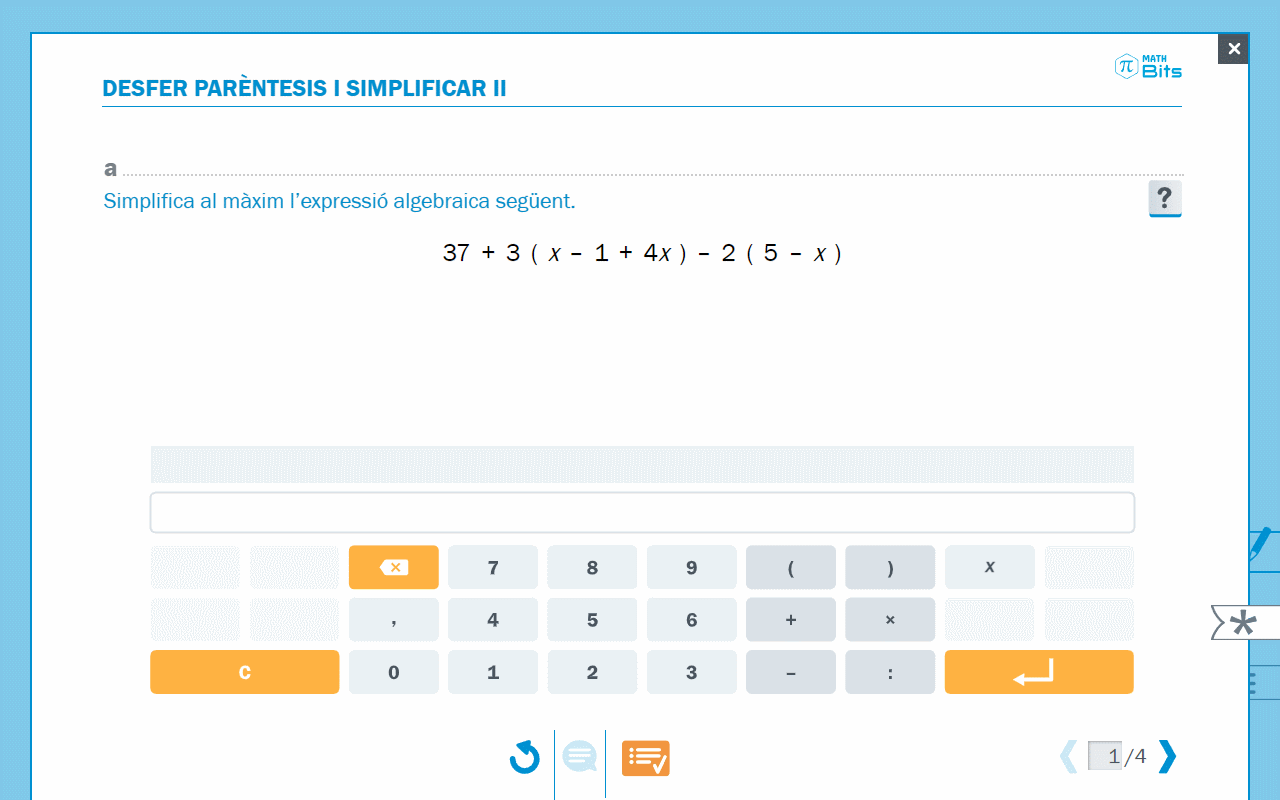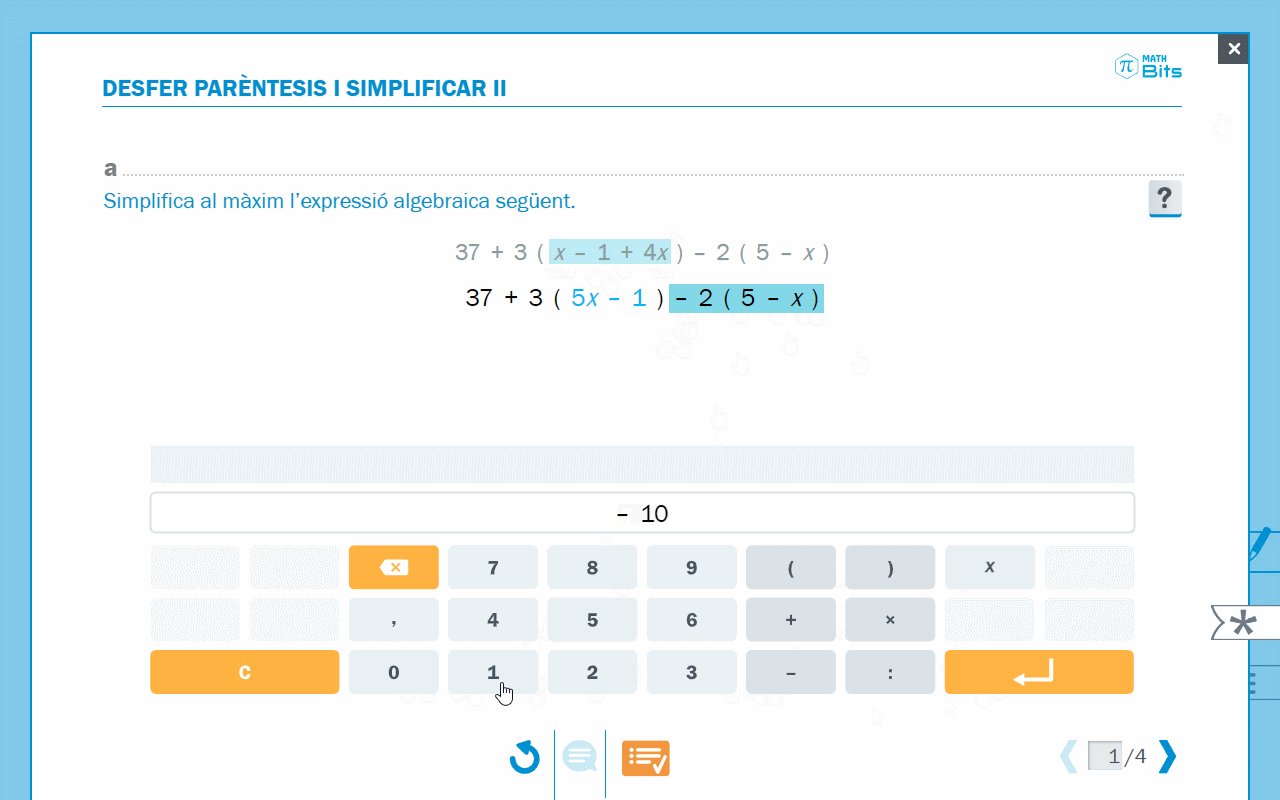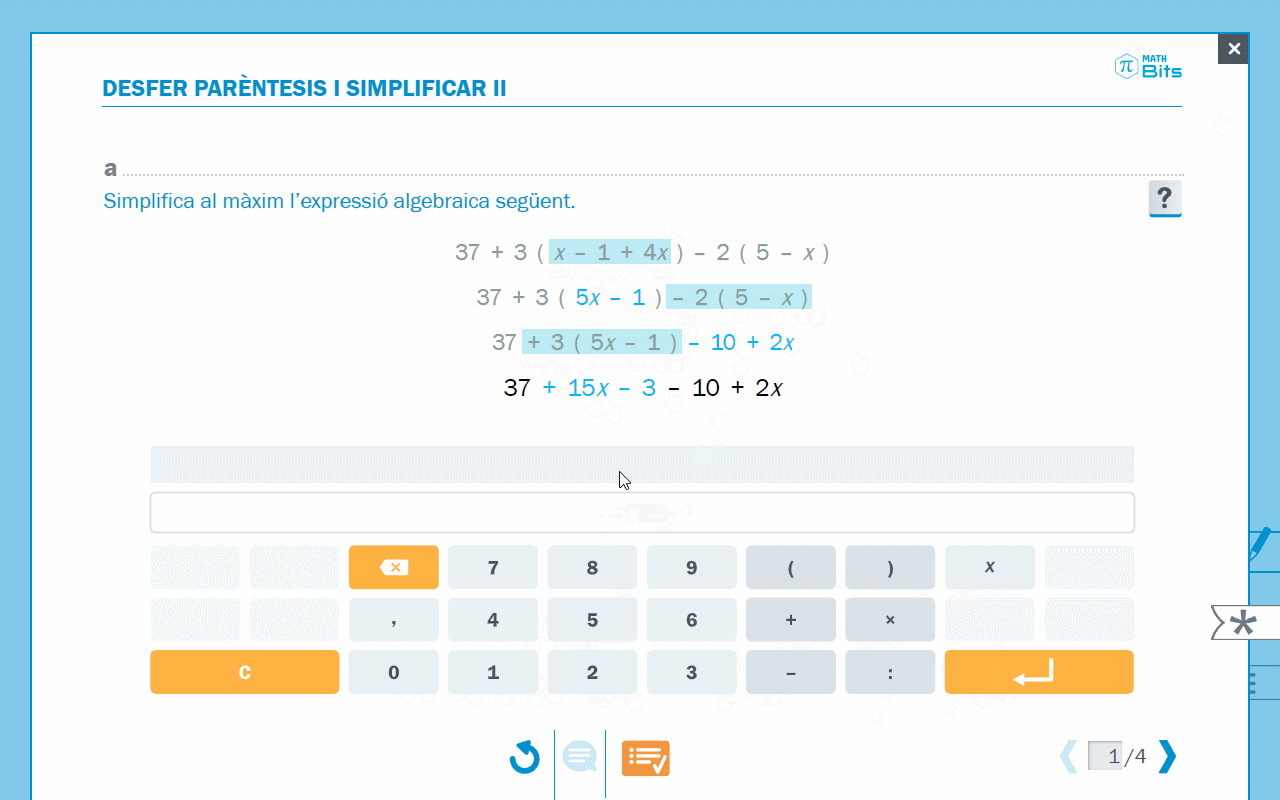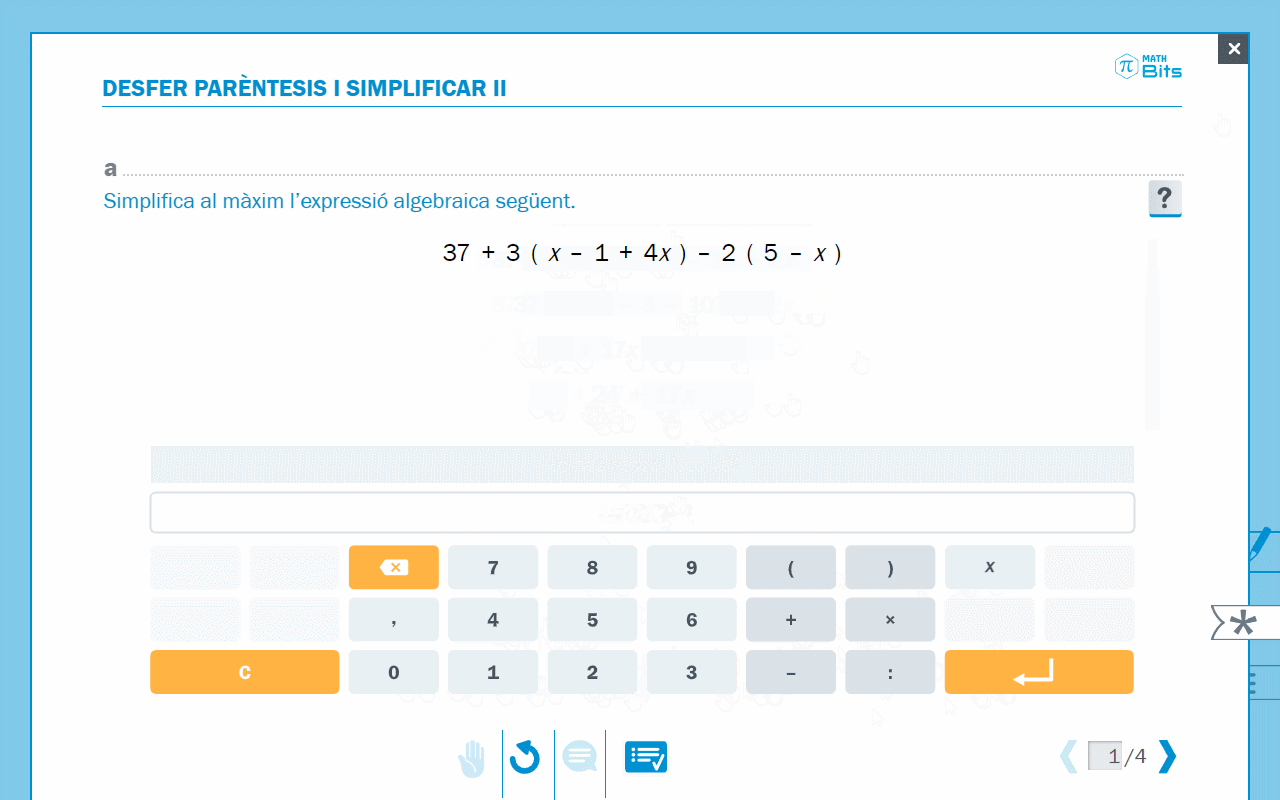
- Editor per a simplificar expressions algebraiques
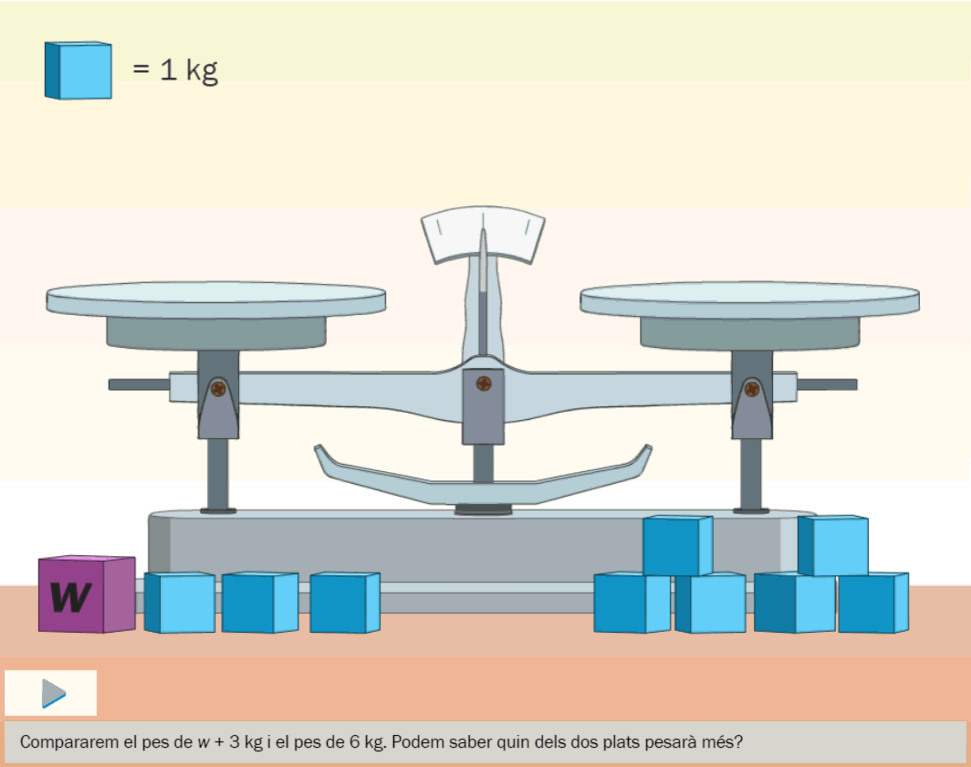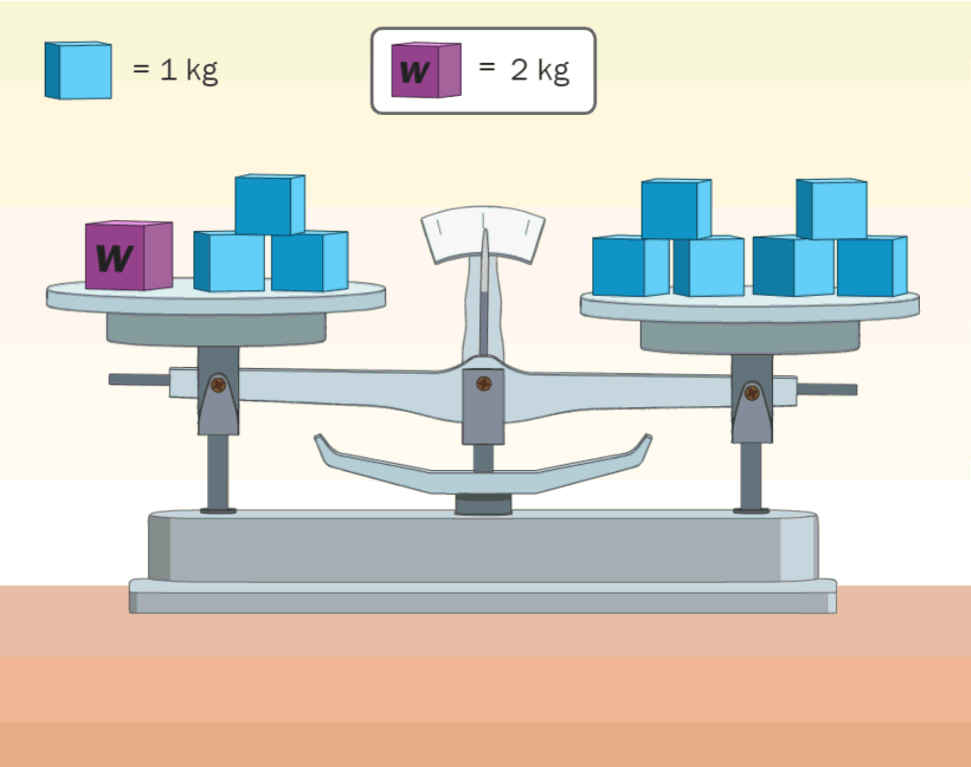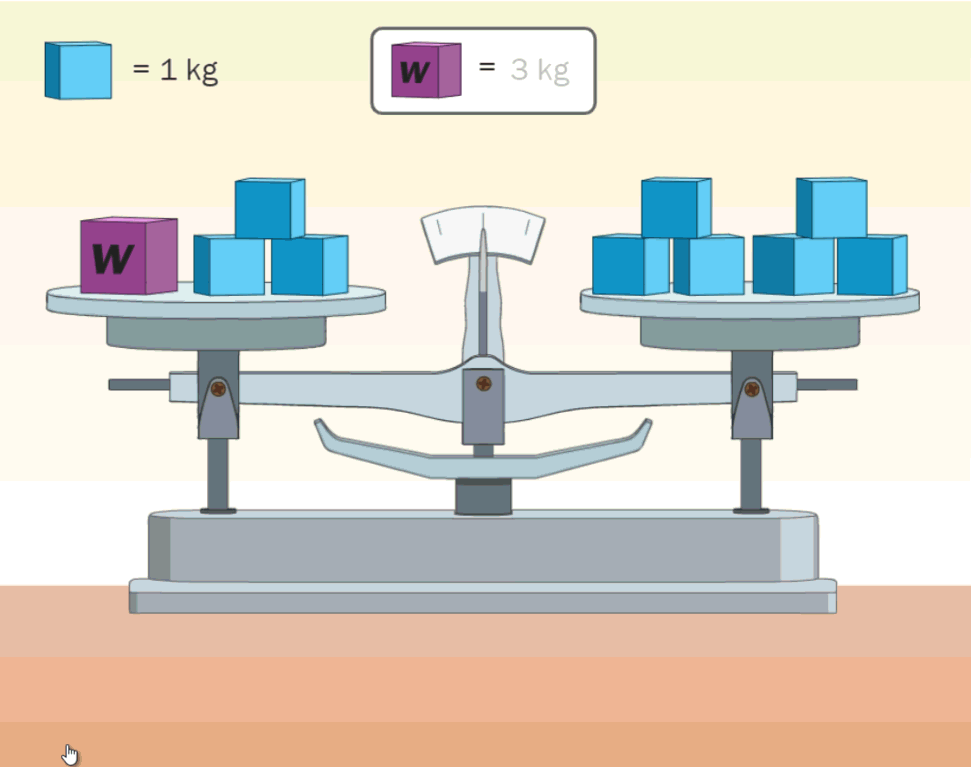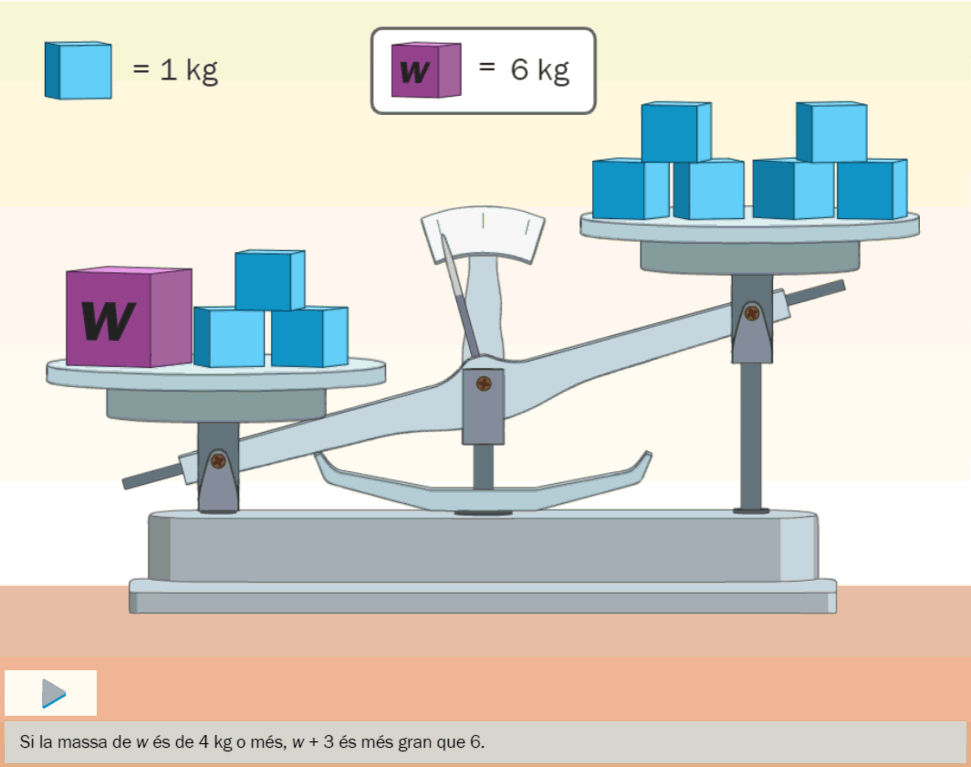
- Animacions per a interpretar la comparació d’expresions algebraiques.
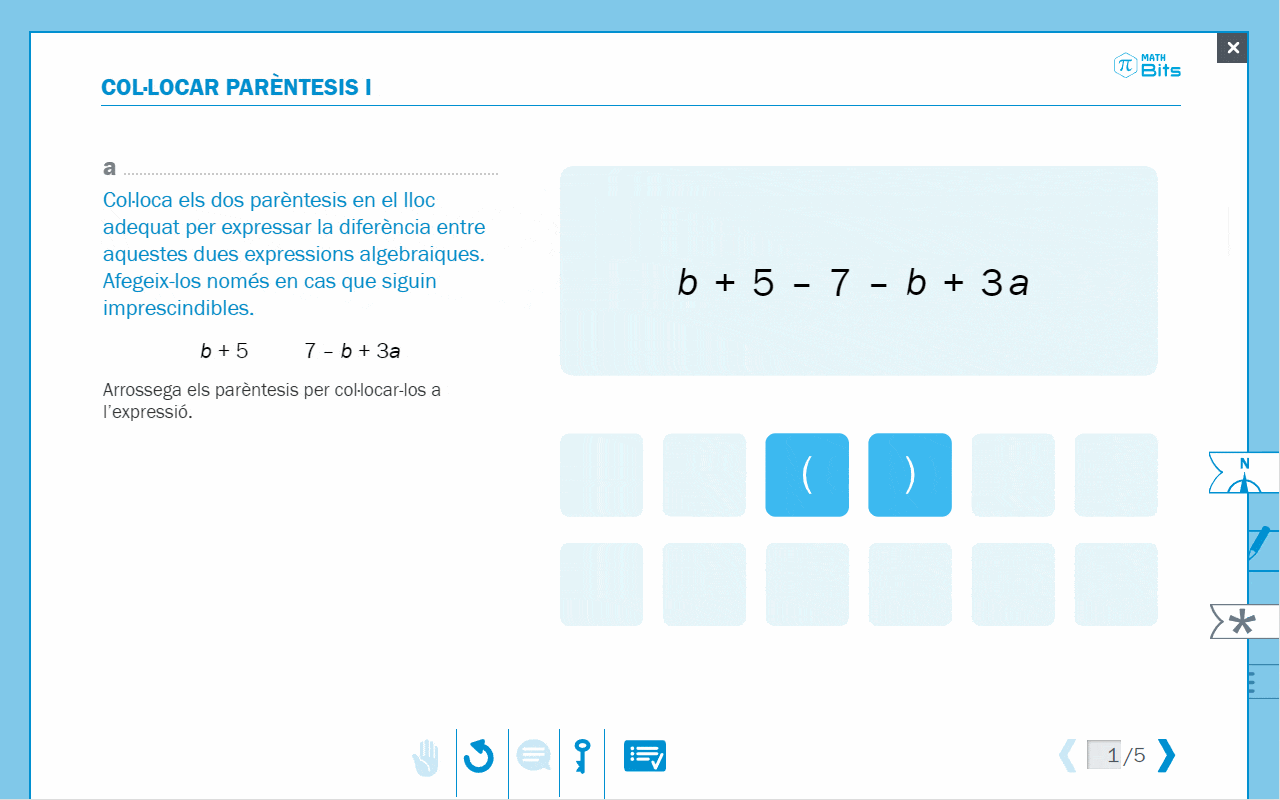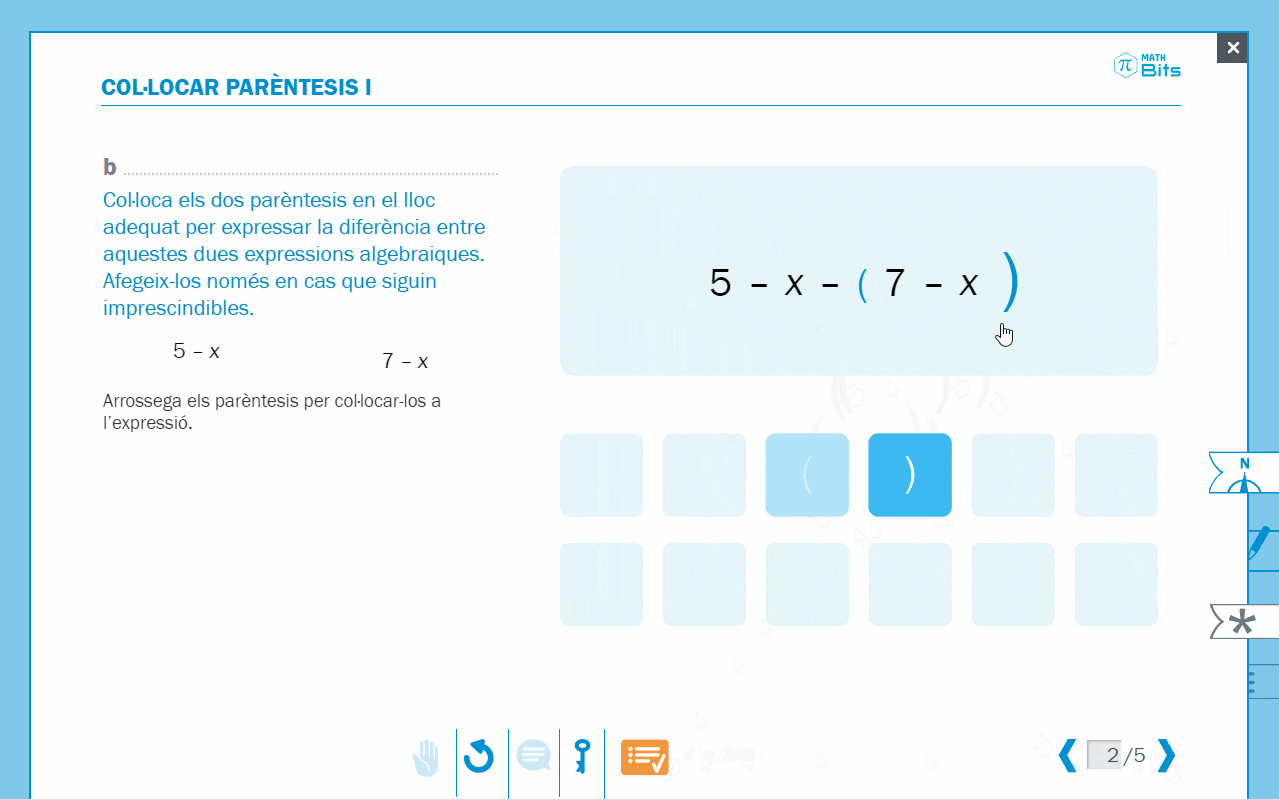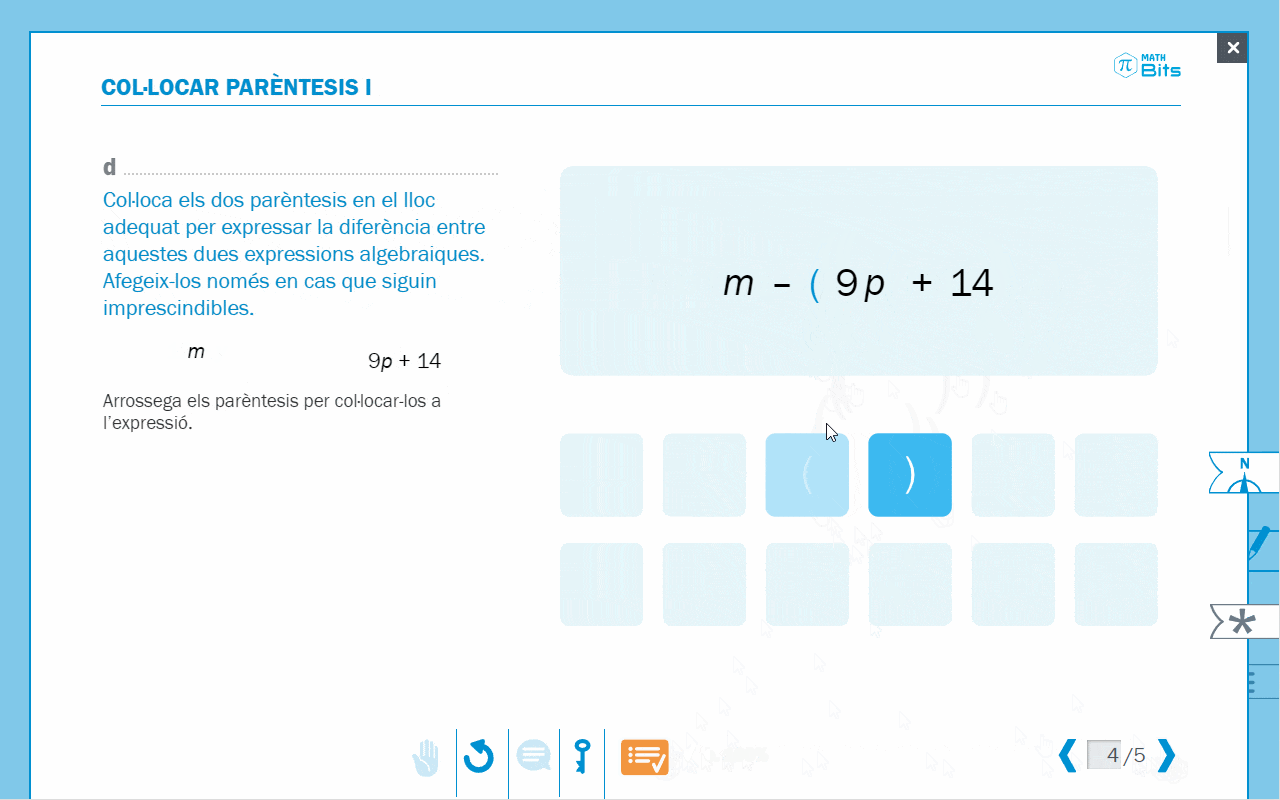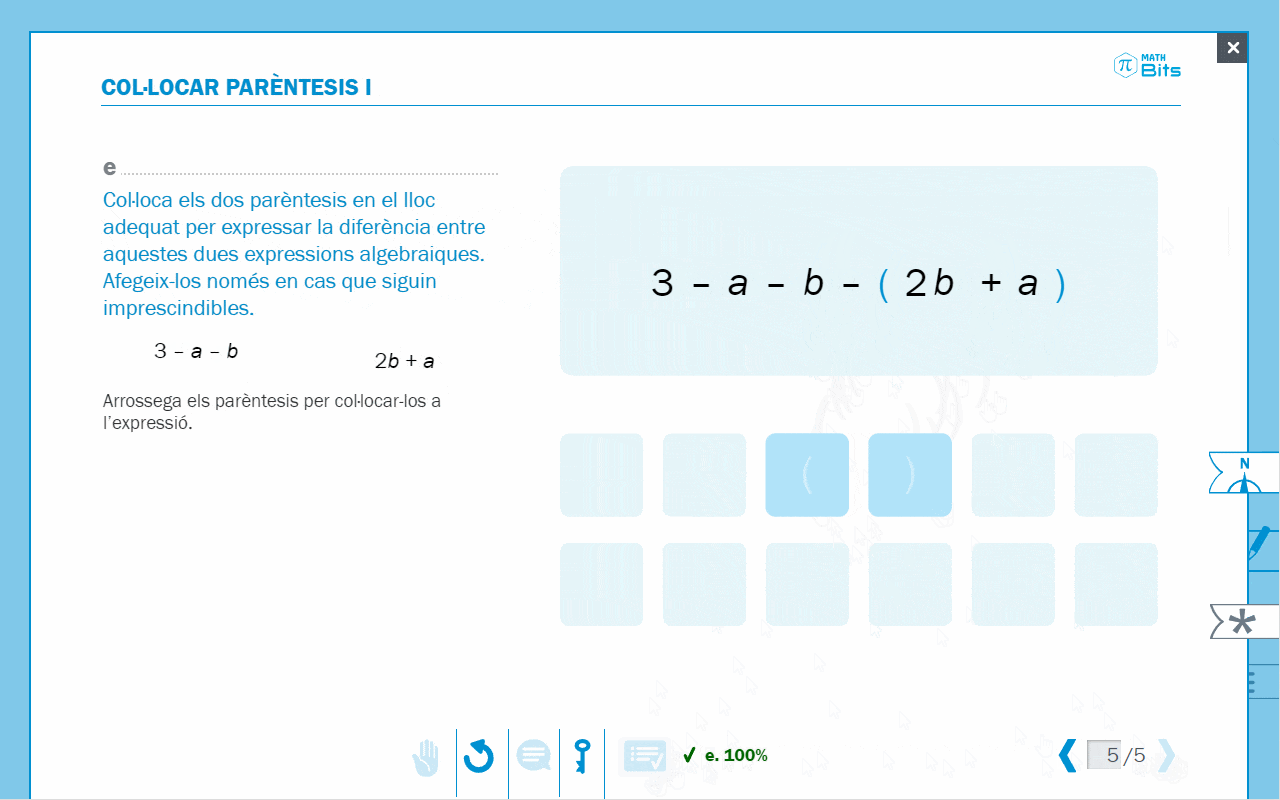
- Exercici de col·locació de parèntesis per expressar diferències entre expressions algebraiques.
- Recursos interactius per a comprendre que hi ha igualtats i desigualtats que poden ser certes o falses en funció del valor que s’assigni a la variable.
- Joc d’adivinació [matemàtica/basat en àlgebra].
Animació on s’observa la simplificació d’expressions algebraiques.















Deixa un comentari