
Les unitats de Math Bits conclouen amb tres lliçons de tipus avaluatiu que remarquen la importància d’utilitzar l’avaluació per aprendre. Malgrat que totes les activitats en totes les fases anteriors ja comporten una avaluació contínua, l’objecte d’acabar la lliçó amb tres activitats explícitament avaluatives, enfocades en els mateixos objectius d’aprenentatge i amb una dificultat semblant, té la seva raó de ser. Aquesta proposta es basa en els principis del mastery learning (mètode que considera que el procés d’aprenentatge no finalitza amb una prova d’avaluació, sigui quin sigui el resultat, sinó que proposa continuar aquest procés fins que el resultat sigui satisfactori) i de l’«avaluació per a l’aprenentatge» (o avaluació formativa), que entenen l’avaluació com un procés d’aprenentatge en si mateix.
Per què Math Bits proposa fer tres proves al final de cada unitat?
Comencem pel més bàsic: quan l’avaluació és explícita, els estudiants donen més rellevància a la tasca i hi presten més atenció. Ara bé, el fet d’oferir múltiples oportunitats per avaluar el seu assoliment redueix l’ansietat que alguns alumnes experimenten davant de les proves, atès que aprecien que el risc en cadascuna d’elles es dilueix. Això els permet enfocar-se més en la prova, cosa que repercuteix en el seu assoliment i en l’aprenentatge que obtenen en fer-la. A més, com que les tres proves aborden els mateixos objectius d’aprenentatge, els estudiants entenen que tindran l’ocasió d’esmenar els seus errors en noves oportunitats. Això no solament redueix l’ansietat, sinó que fa que l’atenció al feedback, que podem proporcionar entre una prova i l’altra, es multipliqui.
Efectivament, una de les millors maneres d’aplicar aquesta avaluació múltiple consisteix a dedicar sessions intermèdies entre cada prova per proporcionar feedback formatiu. Podem fer-ho de diverses maneres:
- Oferint explicacions a tota la classe sobre les activitats que hagin comportat més dificultats (podem identificar-les fàcilment a partir de les dades de la correcció automàtica).
- Activant el feedback que contenen totes les activitats de Math Bits i instigant els estudiants a revisar-lo.
- Posant en joc estratègies d’aprenentatge cooperatiu, en què els estudiants que hagin resolt bé unes activitats ajudin els que hagin tingut problemes. Aquesta pràctica resulta especialment desitjable, atès que se’n beneficien tant els estudiants que reben l’ajuda com els que la presten. En efecte, la recerca en aprenentatge cooperatiu mostra que quan un estudiant ensenya els seus companys aconsegueix que els seus coneixements esdevinguin més profunds, duradors i transferibles.
El feedback és un dels factors que té més efecte en l’aprenentatge, però perquè sigui així és necessari que l’estudiant n’apreciï la utilitat. Com hem apuntat prèviament, això és el que aconseguim amb les múltiples proves que avaluen els mateixos objectius d’aprenentatge, atès que d’aquesta manera l’estudiant entén que el feedback el pot ajudar a afrontar l’oportunitat següent.
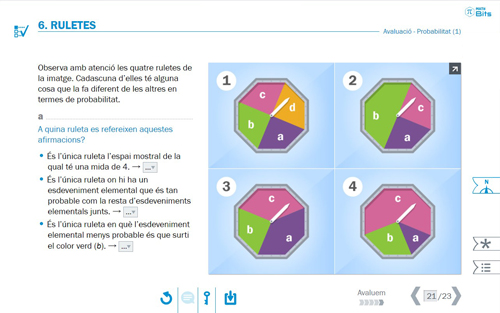
Activitats avaluatives al final de cada lliçó.
La idea d’una avaluació múltiple també contribueix a millorar les creences que els estudiants tenen sobre com funciona l’aprenentatge i com es veuen ells en qualitat d’aprenents. Això és així perquè l’oportunitat de posar a prova la seva destresa més d’un cop els permet apreciar (amb fets i no solament amb paraules) que cometre un error no és una evidència d’una suposada incapacitat per aprendre, sinó un element intrínsec del procés d’aprenentatge, del qual poden aprendre per superar-se. Per tant, aquesta avaluació fa possible que l’alumne estigui més obert a aprendre d’una de les fonts més importants d’aprenentatge: els errors.
Amb tot, aquesta manera d’avaluar no contribueix tan sols a l’aprenentatge pels motius exposats, sinó que també té altres beneficis implícits. En efecte, una de les revelacions més interessants de les ciències cognitives sobre com aprenem és que avaluar-se, per se, és una de les accions que més ens ajuden a aprendre.
L’avaluació, doncs, implica evocar allò après (recuperar-ho de la nostra memòria), i la recerca científica constata que aquesta acció és una de les que més ajuden a consolidar l’aprenentatge i fer-lo així més durador, transferible, funcional i productiu. En altres paraules, quan fem l’esforç d’evocar un coneixement, ja sigui factual, conceptual o procedimental, millorem la capacitat d’evocar-lo de nou més endavant, molt més que si el tornem a consultar. Per tant, el fet d’avaluar allò que s’ha après no solament serveix per comprovar si l’aprenentatge s’ha produït, sinó que en realitat és un acte d’aprenentatge en si mateix (dels més eficaços, certament). Avaluar-se és aprendre.
Addicionalment, el fet de practicar amb els mateixos objectius d’aprenentatge diverses vegades però de manera espaiada en el temps també contribueix com poques coses a consolidar l’aprenentatge. Aquí és important remarcar que es tracta d’oportunitats per practicar que es produiran en sessions diferents, entre les quals, a més a més, l’alumne tindrà l’oportunitat de rebre feedback sobre la prova anterior.
Però això no és tot: els beneficis d’aquest tipus d’avaluació augmenten si les proves promouen l’anomenada pràctica entrellaçada. Es tracta d’organitzar les activitats de manera que els estudiants hagin d’aplicar els diversos aprenentatges que han fet de manera combinada, sense pistes supèrflues per resoldre les qüestions, com les que ofereix el fet de saber a quin tema o apartat correspon l’activitat. Això flexibilitza l’aprenentatge i el fa més sòlid i transferible. De fet, la pràctica entrellaçada és una altra de les estratègies d’aprenentatge més eficaces en l’àmbit de les matemàtiques.
En definitiva, quan s’utilitza adequadament, l’avaluació pot ser una de les eines més eficaces per promoure l’aprenentatge.
Més informació: Math Bits, activa les teves classes de matemàtiques
ESCRIT PER
Héctor Ruiz Martín – ISTF
@hruizmartin
Referències:
- Bjork, E. L., y Bjork, R. A. (2011). Making things hard on yourself, but in a good way: Creating desirable difficulties to enhance learning. En: M. A. Gernsbacher, R. W. Pew, L. M. Hough y J. R. Pomerantz (Eds.), Psychology and the real world: Essays illustrating fundamental contributions to society (pp. 59-68). Nueva York, EE. UU.: Worth Publishers.
- Carpenter, S. K. (2014). Spacing and interleaving of study and practice. En: V. A. Benassi, C. E. Overson y C. M. Hakala (Eds.), Applying the science of learning in education: Infusing psychological science into the curriculum (pp. 131-141). Washington D. C., EE. UU.: Society for the Teaching of Psychology.
- Hattie, J., y Timperley, H. (2007). The power of feedback. Review of Educational Research, 77(1), 81-112.
- Karpicke, J. D., y Roediger, H. L. (2008). The critical importance of retrieval for learning. Science, 319(5865), 966-968.
- Sanmartí, N. (2007). Evaluar para aprender. Barcelona, Espanya: Graó.
- Slavin, R. E. (2013). Cooperative learning and achievement: Theory and research. En: W. M. Reynolds, G. E. Miller y I. B. Weiner (Eds.), Handbook of psychology: Educational psychology (2.ª edición, vol. 7, pp. 199-212). Hoboken, EE. UU.: John Wiley & Sons Inc.
- Wiliam, D. (2011). Embedded formative assessment. Bloomington, EE. UU.: Solution Tree Press.













Deixa un comentari